longitudinal speed planning

ref:

• 2019-Safe Trajectory Generation for Complex Urban Environments Using Spatio-temporal Semantic Corridor
• 2014-Minimum-time speed optimisation over a fixed path.
• 2013-Optimal Longitudinal Control Planning with Moving Obstacles
• 2021-Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform
• Tunable and Stable Real-Time Trajectory Planning for Urban Autonomous Driving-96
• Efficient Mixed-Integer Programming for Longitudinal and Lateral Motion Planning of Autonomous Vehicles-42

2014-Minimum-time speed optimisation over a fixed path

• global_racetrajectory_optimization

Estimating derivatives of the path

离散近似的阶数对一阶导近似影响不大，对二阶导近似影响较大。

一阶导近似：$s'(\overline\theta_i)=\frac{s(\theta_i)-s(\theta_{i-1})}{d\theta}$

二阶导近似： 下图线是不同近似阶数再积分后对结果的影响

$$\begin{aligned} s^{\prime\prime}\left(\bar{\theta}_{i}\right) &=\frac{s(\theta_{i-2})-2s(\theta_{i-1})+s(\theta_{i})}{d\theta^{2}} \quad \text{(35)} \\ s^{\prime\prime}\left(\bar{\theta}_{i}\right) &=\frac{s(\theta_{i-1})-2s(\theta_{i})+s(\theta_{i+1})}{d\theta^{2}}\quad \text{(36)} \\ s^{\prime\prime}\left(\bar{\theta}_{i}\right)&=\frac{s(\theta_{i-2})-s(\theta_{i-1})-s(\theta_{i})+s(\theta_{i+1})}{2d\theta^{2}} \quad \text{(37)}\\ s^{\prime\prime}\left(\bar{\theta}_{i}\right)&=\frac{-\frac{5}{48}s(\theta_{i-3})+\frac{13}{16}s(\theta_{i-2})-\frac{17}{24}s(\theta_{i-1})-\frac{17}{24}s(\theta_{i+1})-\frac{5}{48}s(\theta_{i+2})}{d\theta^{2}} \quad \text{(38)}\end{aligned}$$

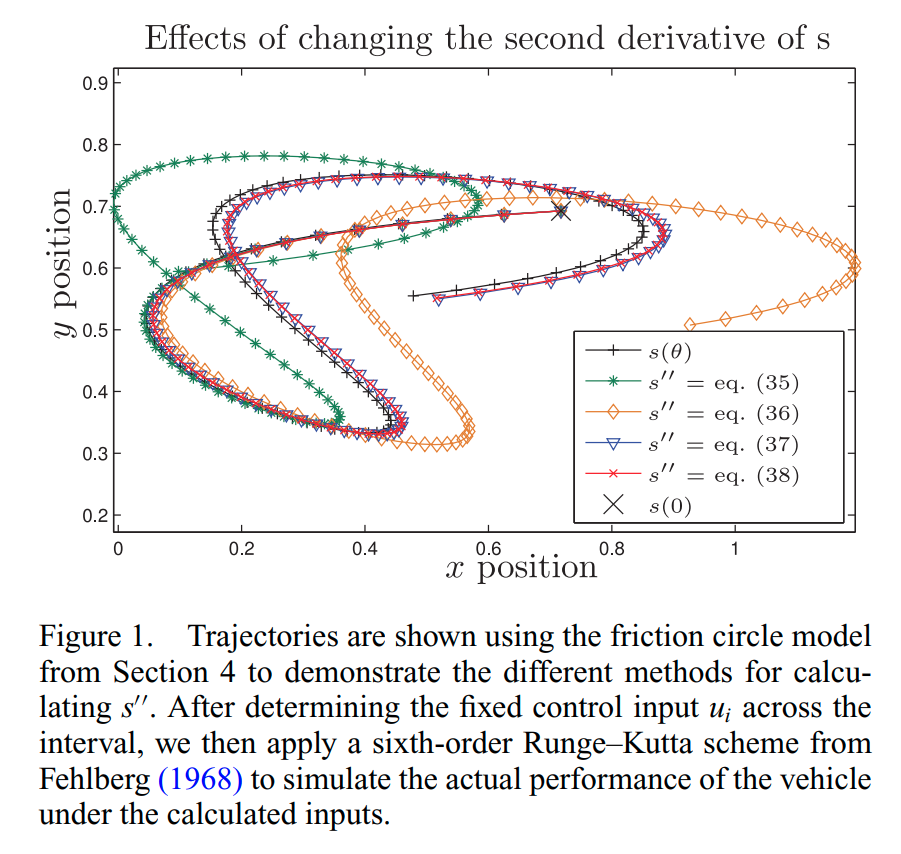
从上图中可以看出，（35）和（36）都是有偏差的二阶模型(second-order models,)，而（37）和（38）偏差不大，分别是对称4阶和6阶模型(symmetric fourth- and sixth-order models). 并且由37）和（38）对比来看，对称4阶以上已经没有太大意义，两者几乎没有差距。因此（37）式子可以作为最优选择。

（37）会用到当前点的前两个点，这对于$\theta_1$会有问题，因此创造一个虚拟点$s(\theta_{-1})=2s(0)-s(\theta_1)$, 由此可得：

$$s^{\prime\prime}(\bar{\theta}_{1})={\frac{{\frac{1}{2}}s(0)-s(\theta_{1})+{\frac{1}{2}}s(\theta_{2})}{d\theta^{2}}}$$