longitudinal speed planning

• spatio-temporal planning
• path-speed decoupled

ref:

• 2019-Safe Trajectory Generation for Complex Urban Environments Using Spatio-temporal Semantic Corridor
• 2014-Minimum-time speed optimisation over a fixed path.
• 2013-Optimal Longitudinal Control Planning with Moving Obstacles
• 2021-Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform
• Tunable and Stable Real-Time Trajectory Planning for Urban Autonomous Driving-96
• Efficient Mixed-Integer Programming for Longitudinal and Lateral Motion Planning of Autonomous Vehicles-42

2019 Spatio-temporal Semantic Corridor

• code

2022 Real-Time Trajectory Planning for Autonomous Driving with Gaussian Process and Incremental Refinement

• paper
• code

planner: Gaussian process(GP)

speed: st-graph

Related

Motion Planning via Probabilistic Inference

GAUSSIAN PROCESS PATH PLANNING

M. Mukadam, X. Yan, and B. Boots, “Gaussian process motion
planning,” in 2016 IEEE Int. Conf. Rob. Autom. (ICRA). IEEE, 2016,
pp. 9–15.
[10] M. Mukadam, J. Dong, X. Yan, F. Dellaert, and B. Boots, “Continuoustime Gaussian process motion planning via probabilistic inference,”
Int. J. Rob. Res, vol. 37, no. 11, pp. 1319–1340, 2018.
[11] M. Werling, S. Kammel, J. Ziegler, and L. Groll, “Optimal trajectories ¨
for time-critical street scenarios using discretized terminal manifolds,”
Int. J. Rob. Res., vol. 31, no. 3, pp. 346–359, 2012

SPEED-PROFILE GENERATION

s-t graph search

1. trajectory projection

2. forward expansion $$\left[\begin{array}{c} s_{i+1}^j \\ \dot{s}_{i+1}^j \end{array}\right]=\left[\begin{array}{c} s_i+\dot{s}_i T_f+\frac{1}{2} a_j T_f^2 \\ \dot{s}_i+a_j T_f \end{array}\right], 1 \leq j \leq k .$$

3. local truncation: 局部剔除cost比较大的点

s-t curve smoothing

fit the coarse speed-profile with a piecewise Bezier curve and ´ construct the overall problem as a quadratic programming (QP).

与apollo 基于spline的st图优化方式同。

2020 Baidu Apollo PJSO

• path-speed decoupled
• DL-IAPS: Dual-Loop Iterative Anchoring Path Smoothing, for collision avoidance and path smoothing
• PJSO: Piece-wise Jerk Speed Optimization

Path planning

碰撞检测：如果有碰撞则向内缩小

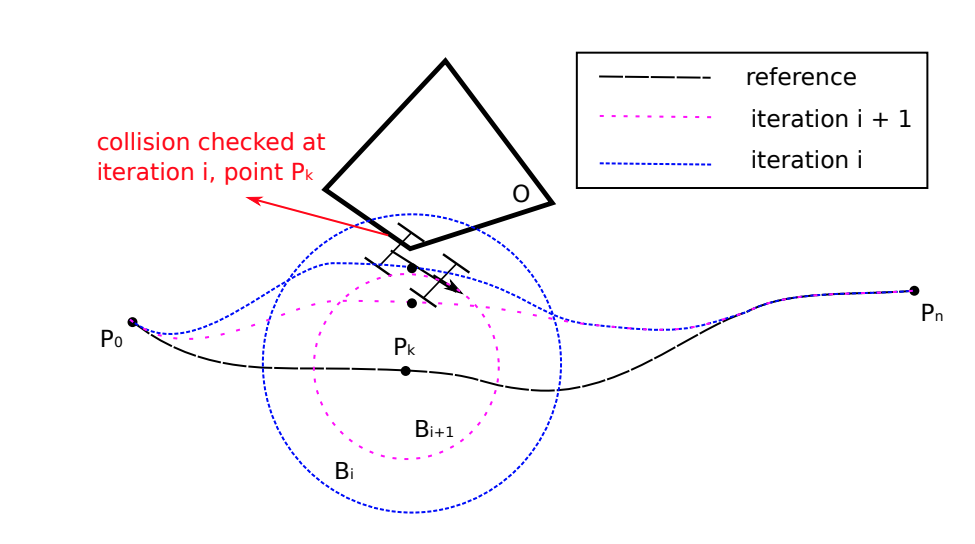
Speed planning

• 均匀离散t
• $s,\dot{s}, \ddot{s}作优化变量$

$$\begin{aligned} & \min _{s, \dot{s}, \ddot{s}} \mathcal{J}_c(s, \dot{s}, \ddot{s})=w_{s_f} \sum_{k=0}^{n-1}\left(s_k-s_f\right)^2 \\ & \quad+w_{ddds} \sum_{k=0}^{n-2}\left(\left(\ddot{s}_{k+1}-\ddot{s}_k\right) / \Delta t\right)^2+w_{\ddot{s}} \sum_{k=0}^{n-1} \ddot{s}_k^2, \\ & \text { subject to: } \\ & \qquad\left[s_0, \dot{s}_0, \ddot{s}_0\right]=[0.0,0.0,0.0] \\ & \quad\left[s_j, \dot{s}_j, \ddot{s}_j, \frac{\ddot{s}_{j+1}-\ddot{s}_j}{\Delta t}\right] \in \mathcal{S}, \\ & \quad \dot{s}_j<\sqrt{a_{lateral\_max}\kappa(s)_{\max }}, \\ & \quad \dot{s}_{k+1}=\dot{s}_k+\frac{1}{2} \ddot{s}_k \Delta t+\frac{1}{2} \ddot{s}_{k+1} \Delta t, \\ & s_{k+1}=s_k+\dot{s}_k \Delta t+\frac{1}{3} \ddot{s}_k \Delta t^2+\frac{1}{6} \ddot{s}_{k+1} \Delta t^2, \\ & \quad \text { for } k=0, \ldots, n-2, j=0, \ldots, n-1, \\ & \quad \text { and } n=r \frac{v_{\max }^2+s_f a_{\max }}{a_{\max } v_{\max } \Delta t} . \end{aligned}$$

运动学约束：

$$\begin{aligned}\dot{s}_{k+1} & =\dot{s}_k+\ddot{s}_k \Delta t+\frac{1}{2} ddds_{k, k+1} \Delta t^2 \\ & =\dot{s}_k+\frac{1}{2} \ddot{s}_k \Delta t+\frac{1}{2} \ddot{s}_{k+1} \Delta t, \\ s_{k+1} & =s_k+\dot{s}_k \Delta t+\frac{1}{2} \ddot{s}_k \Delta t^2+\frac{1}{6} ddds_{k, k+1} \Delta t^3 \\ & =s_k+\dot{s}_k \Delta t+\frac{1}{3} \ddot{s}_k \Delta t^2+\frac{1}{6} \ddot{s}_{k+1} \Delta t^2 . \end{aligned}$$

曲率约束：

近似表达

$$\dot{s}_j<\sqrt{a_{lateral\_max}\kappa(s)_{\max }}$$

参数估计：

$T_{horizon} = n\Delta t$, 估计 $n$

$$n_{min} = \frac{v^2_{max}+s_f s_{max}}{a_{max}v_{max}\Delta t} \\ n = r *n_{min}\\ r: heuristic expansion ratio, [1.2,1.5]$$

尽快到达：

惩罚s与目标s的差 $$\sum_{k=0}^{n-1}(s_k-s_f)^2$$

2017 Speed Profile Planning in Dynamic Environments via Temporal Optimization

paper

• SCFS： the slack convex feasible set algorithm

• code

Introduction

• planning framework:
  • integrated framework relies on spatiotemporal planning
  • seperated framework: path first, speed second

Problem Formulation

st 图构建： 遍历s进行构建，所以可通行区域是横的。如此，$s_i$是固定量，$t_i$是优化变量.运动学变量都可以通过上述的$s_i,t_i$来描述数。而障碍物约束通过控制$t_i$的上下限来实现。

• speed profile: $\mathcal{V}=\left{\left(T_i, s_i\right)\right}_i$
• $p_i:=p(s_i)$
• $v_i:=v(t_i)$
• $a_i:=a(t_i)$
• $j_i:=j(t_i)$

(homotopy / hoʊməˈtɑːpi / 同伦 )

运动学计算：

$$v_i=\frac{p_{i+1}-p_i}{t_i}, a_i=\frac{2\left(v_i-v_{i-1}\right)}{t_i+t_{i-1}}, j_i=\frac{3\left(a_i-a_{i-1}\right)}{t_i+t_{i-1}+t_{i-2}} .$$

lateral acceleration and longitudinal acceleration

优化方程：

$$\begin{aligned} \min _{t_1, \cdots, t_h} & w_1 \sum\left|a_i^\tau\right|^2+w_2 \sum\left|a_i^\eta\right|^2+w_3 \sum\left|j_i^\tau\right|^2 \\ & +w_4 \sum\left|j_i^\eta\right|^2+w_5 \sum\left(v^r-v_i^\tau\right)^2 \\ \text { s.t. } & T_i \in\left[T_i^{\text {min }}, T_i^{\text {max }}\right] \\ & a_i \in \Omega, \end{aligned}$$

QUADRATIC APPROXIMATION

transform origin problem into a sequence of quadratic programs in the framework of the SCFS algorithm

rearrange:

• 边界条件
• 运动学约束 把关于t的因子抽取出来

SCFS： 把非退化的非线性等是约束转化为非线性不等式约束

1. non degenerating（非退化）：在优化理论中，如果在最优解处约束条件是线性无关的，那么我们常说这个问题是非退化的。 "非退化"在优化问题中常常意味着约束条件在最优解处是"清晰的"或者"充分的"，且没有冗余的限制

• 2016 Geometric considerations on real time trajectory optimization for nonlinear systems

2018 Toward a More Complete, Flexible, and Safer Speed Planning for Autonomous Driving via Convex Optimization

• blog- Convex-optimization-based Speed Planning

从ST图转到TS图？

It cannot handle multiple dynamic obstacles in optimization directly

Motivation

constraints for speed planning

• safety
• smooth
• time-efficient

$$\begin{array}{llll} \hline \text { Category } & \text { Constraint Name } & \text { Description } & \text { Property } \\ \hline \text { Soft Constraints } & \begin{array}{l} \text { Smoothness (S) } \\ \text { Time Efficiency (TE) } \end{array} & \begin{array}{l} \text { continuity of speed, acceleration and jerk over the path } \\ \text { time used by travelling along the path } \end{array} & \begin{array}{l} \text { performance } \\ \text { performance } \end{array} \\ \hline \text { Hard Constraints } & \text { Friction Circle (FC) } & \text { total force should be within the friction circle } & \text { safety } \\ & \text { Time Window (TW) } & \text { time window to reach a certain point on path } & \text { safety } \\ & \text { Boundary Condition (BC) } & \text { speed at the end of the path } & \text { safety\&performance } \\ \hline \end{array}$$

dynamics

$$\begin{aligned} \theta & \text { heading of the car } \\ u^{\tau} & \text { lateral force in ego frame } \\ u^{\eta} & \text { longitudinal force in ego frame } \\ \text{prime } &'\text{: derivative eith respact to arc-length s} \\ \text{dot } &\dot{}\text{ :derivative eith respact to time t } \end{aligned}$$

path representation

• $\dot{f} $: relative to time
• $r' $: relative to s

$$\begin{aligned} r(s)&=(x(s), y(s)), s \in\left[0, s_{f}\right] \\ r'(s)&=(cos(\theta), sin(\theta(s)))=(x'(s), y'(s))\\ s & =f(t) \\ \alpha(s) & =\ddot{f} \quad \text{longitudinal acceleration} \\ \beta(s) & =\dot{f}^2 \quad \text{square of the longitudinal speed} \\ \beta^{\prime}(s)&=2 \alpha(s), s \in\left[0, s_f\right] \end{aligned}$$

dynamics:

• $r'(s)$ 实际上代表了路径s的单位切向量, 表示速度的方向
• $r''(s)$ principal normal vector of the path, or curvature vector. its 2-norm is the scalar of the curvature

$$\begin{aligned} \vec{v}=\dot{r}(s)&=r^{\prime}(s) \dot{f}\\ \overrightarrow{\boldsymbol{a}}=\ddot{r}(s)&=r^{\prime \prime}(s) \dot{f}^2+r^{\prime} \ddot{f} \\ \dot{x}(s)&=\frac{\partial x}{\partial s} \dot{f} \\ \ddot{x}(s)&=\frac{\partial^2 x}{\partial s^2} \dot{f}^2+\frac{\partial x}{\partial s} \ddot{f} \\ &=x''(s)\beta(s)+x'(s)\alpha(s) \end{aligned}$$

$$\text { Dynamics }\left\{\begin{array}{l} R \boldsymbol{u}=m \ddot{r}(s), \text { dynamics equation } \\ \ddot{r}(s)=r^{\prime \prime}(s) \beta(s)+r^{\prime}(s) \alpha(s) \\ R=\left[\begin{array}{cc} \cos (\theta(s)) & -\sin (\theta(s)) \\ \sin (\theta(s)) & \cos (\theta(s)) \end{array}\right], \text { rotation matrix } \\ \boldsymbol{u}=\left(u^{\tau}, u^{\eta}\right), \text { control vector } \end{array}\right.$$

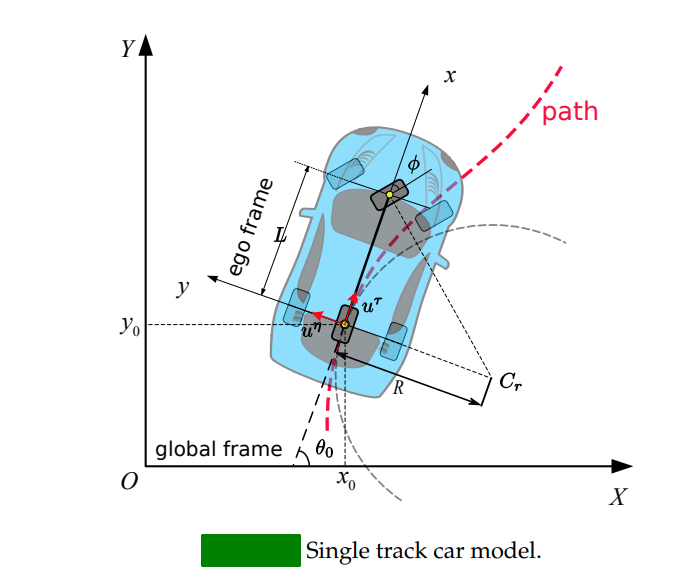
friction circle constraints:

$$\begin{gathered} (\alpha(s), \beta(s), \boldsymbol{u}(s)) \in\left\{\left(\ddot{r}(s), \dot{r}^2(s), \boldsymbol{u}(s)\right) \mid\right. \\ \|\boldsymbol{u}(s)\| \leq \mu m g, \quad \text{tire friction drive force} \\ u^\tau(s) \leq m \cdot a_{\max }^\tau \quad \text{max lon acc constraint} \\ \left.\beta(s) \leq v_{\max }^2\right\} . \quad \text{velocity constraint} \end{gathered}$$

object function

优化变量：$\alpha(s), \beta(s), \mu(s)$

object function is viewed as soft constraints, and constrains function is viewed as hard constraints

• time efficiency: $$J_{T}=T_{s_{f}}=\int_0^{T} 1dt\\ =\int_{f(0)}^{f(t_f)} \frac{1}{\dot{f}}ds=\int_{0}^{s_{f}} \beta(s)^{-\frac{1}{2}} d s$$

• IoD(Integrate of difference) objective: velocity track.(这里是速度跟踪，也许能把它换成速度范围，在下面path constraints有所体现) $$J_v=\int^{s_f}_0||\beta(s)-v_r(s)^2||ds$$

• smooth objective:

  • jerk is common used but is non-convex

  $$\begin{aligned} \mathcal{J}(s) &=\frac{\partial^3 f}{\partial t^3}=\dot{\alpha}(s)=\alpha^{\prime}(s) \dot{f} \\ &=\alpha^{\prime}(s) \sqrt{\beta(s)}=\frac{1}{2} \beta^{\prime \prime}(s) \sqrt{\beta(s)} \end{aligned}$$

  • pseudo jerk, is convex (used in this paper)

  $$J_{S}=\int_{0}^{s_{f}}\left\|\alpha^{\prime}(s)\right\|^{2} d s$$ - path constraints: $\psi(s,x,u)\leq0, s\in[0,s_f]$ - 与轨迹段相关的约束 - $x$是当前状态 - speed limits(与前述IoD约束不同)：$\beta\left(s_i\right) \leq \bar{\beta}\left(s_i\right), \forall s_i \in\left[s_m, s_n\right]$ - boundary condition constraints - zero speed: fully stop in front of obstacle - fixed speed: merge

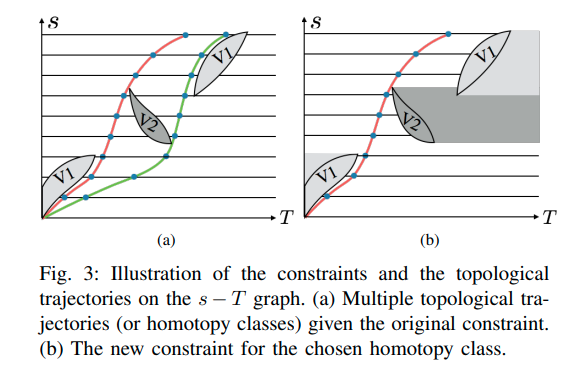
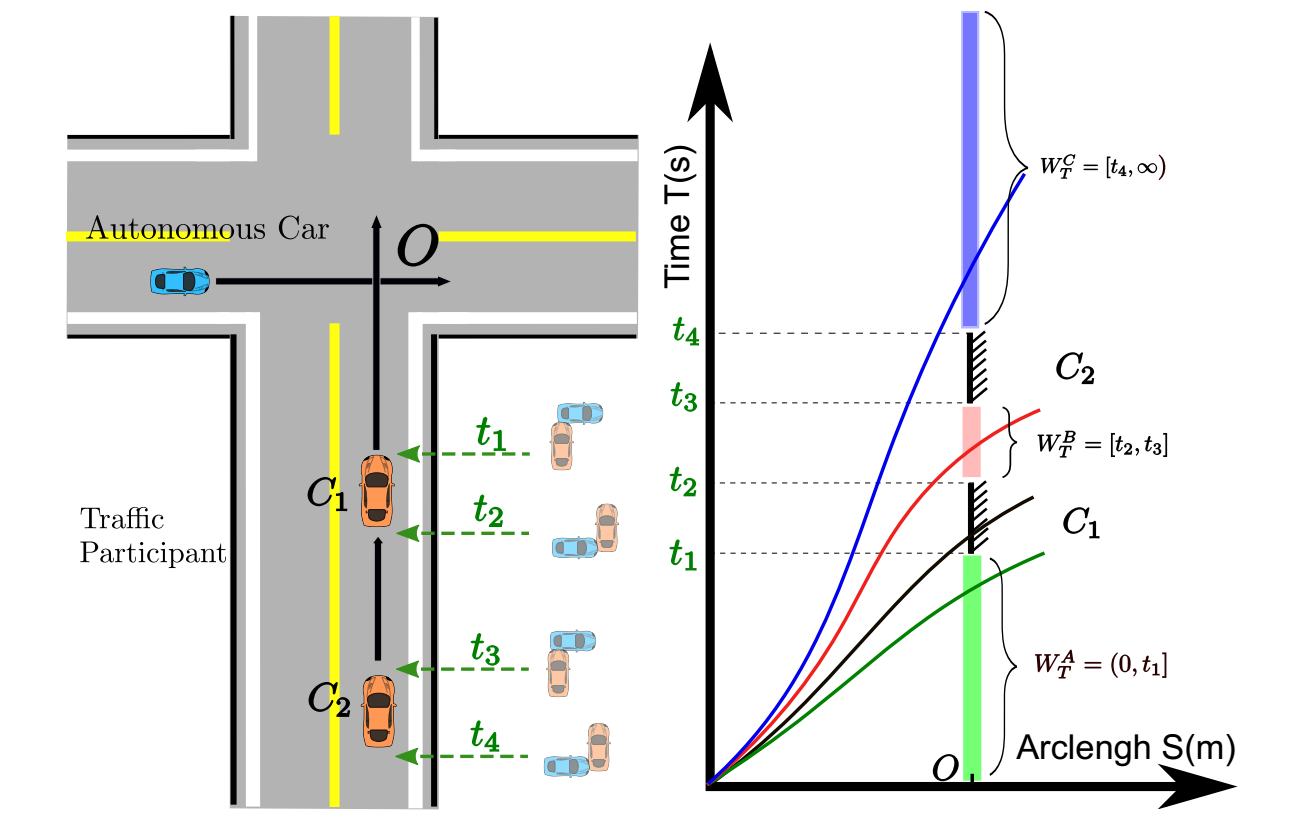
  $$\begin{aligned} & \underline{\alpha}_{s_f} \leq \alpha_{s_f} \leq \bar{\alpha}_{s_f} \\ & \underline{\beta}_{s_f} \leq \beta_{s_f} \leq \bar{\beta}_{s_f} . \end{aligned}$$ - time window constraints: avoid collision with the predicted trajectory of obstacles. 在$\dot{s}-s$图上，通过某段路程的时间被限制在某一个范围内。 $$T_{i}=\int_{0}^{s_{i}} \beta(s)^{-\frac{1}{2}} d s \in\left(0, T_{U}\right]$$

在该图的横穿场景中，两辆车把同行时间分成了三段。其中A段只有一个上限，B段有上下限，C段有一个下限，三段联合组成了这一位置的时间窗口约束。这里只有A段是凸的而B，C是非凸的条件。一般是通过决策过程选择一端把该问题变成凸问题。

• comfort box constraints: use semi-hard constraint. 这里跟动力学的区别是，动力学边界约束保证安全，而这里面的约束只是为了舒适性，所以这里的$a_c^\tau$和$a_{max}^\tau$不是同一个数值。 这里的$\sigma$使得舒适性的加速度限制不再是一个绝对量，而是可调节的。在一般情况下尽量舒适。在不能舒适保持安全的情况下则可以超越限制。

$$\begin{aligned} \left\|a_i^\eta\right\| & \leq a_c^\eta \\ \left\|a_i^\tau\right\| & \leq a_c^\tau, \end{aligned} \Rightarrow \|\alpha(s)\| \leq a_c^\tau+\sigma^\tau(s)$$

the final problem:

$$\begin{array}{cl} \underset{\substack{\alpha(s), \beta(s), u(s), \sigma^\tau(s), \sigma^\eta(s)}}{\operatorname{minimize}} & J=\omega_1 J_T+\omega_2 J_S+\omega_3 J_V \\ & +\lambda_1\left\|\sigma^\tau(s)\right\|+\lambda_2\left\|\sigma^\eta(s)\right\| \\ \text { s.t. } & (6),(8),(11),(17),(19),(20), \\ & \|\alpha(s)\| \leq a_c^\tau+\sigma^\tau(s), \\ & \left\|\frac{u^\eta(s)}{m}\right\| \leq a_c^\eta+\sigma^\eta(s), \\ & 0 \leq \sigma^\tau(s), \\ & 0 \leq \sigma^\eta(s), \end{array}$$

where $\dot{r}^2(s)=\left(r^{\prime}(s)\right)^2 \beta(s) \text { and } \ddot{r}(s)=r^{\prime} \alpha(s)+r^{\prime \prime} \beta(s)$

Implementation with Discretization

$$\beta(s)=\beta_i+\left(s-s_i\right)\left(\frac{\beta_{i+1}-\beta_i}{s_{i+1}-s_i}\right), s \in\left[s_i, s_{i+1}\right] .$$

$$\begin{aligned} J_{T_i} & =\int_{s_i}^{s_{i+1}} \beta(s)^{-\frac{1}{2}} d s \\ & =\int_{s_i}^{s_{i+1}}\left(\beta_i+\left(s-s_i\right)\left(\frac{\beta_{i+1}-\beta_i}{s_{i+1}-s_i}\right)\right)^{-\frac{1}{2}} d s \\ & =\frac{2 \cdot \Delta s}{\sqrt{\beta_i}+\sqrt{\beta_{i+1}}}, \\ J_T& =2 \sum_{i=0}^{N-1} \frac{\Delta s}{\sqrt{\beta_i}+\sqrt{\beta_{i+1}}} \end{aligned}$$

Example

ref

• project
  • Jerk_Bounded_Speed_Planning