自动驾驶中控制优化方法

optimal control

differential dynamic programming

mpc

lqr

代价函数是二次的，而状态方程是线性的

lqr 只看下一时刻，而mpc关注接下来多个时刻

最优控制角度：

全状态反馈控制系统图:

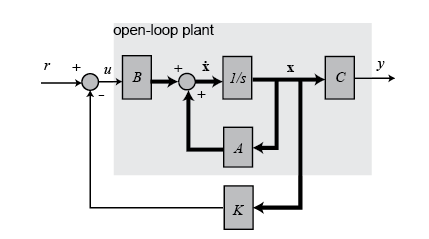
对于系统 $\dot{x}=A x+B u$ , 要设计一个状态反馈控制器 $u=-Kx$ , 则 $\dot{x}=(A-BK)x$ . 因此需要设计K使得能满足要求。

LQR定义了一个能量函数：

$J=\frac{1}{2} \int_{0}^{\infty} x^{T} Q x+u^{T} R u d t$

$Q, R$ 都是半正定矩阵，表示权重参数。这里的x可以看作目标差值，因此最优的时候这个差值是为0的。所以能量函数的两项一个代表了最后的系统稳定，误差为零，第二项代表使用较少的动作。

把 $u=-Kx$ 带入能量函数:

$J=\frac{1}{2} \int_{0}^{\infty} x^{T}\left(Q+K^{T} R K\right) x d t$

假设存在一个常量矩阵P使得： $\frac{d}{d t}\left(x^{T} P x\right)=-x^{T}\left(Q+K^{T} R K\right) x$ , 则可得(这里假设闭环系统稳定，即 $x(t)_{t\rightarrow \inf}\rightarrow$ 0)：

$J=-\frac{1}{2} \int_{0}^{x} \frac{d}{d t}\left(x^{T} P x\right) d t=\frac{1}{2} x^{T}(0) P x(0) \\ \begin{aligned} &\dot{x}^{T} P x+x^{T} P \dot{x}+x^{T} Q x+x^{T} K^{T} R K x=0 \\ &x^{T} A_{c}^{T} P x+x^{T} P A_{c} x+x^{T} Q x+x^{T} K^{T} R K x=0 \\ &x^{T}\left(A_{c}^{T} P+P A_{c}+Q+K^{T} R K\right) x=0 \end{aligned}$

若等于0恒成立，则括号内应为0:

$\begin{aligned} &(A-B K)^{T} P+P(A-B K)+Q+K^{T} R K=0 \\ &A^{T} P+P A+Q+K^{T} R K-K^{T} B^{T} P-P B K=0 \end{aligned}$

若选取 $K=R^{-1} B^{T} P$ 得Riccati方程：

$A^TP+PA+Q-PBR^{-1}B^TP=0$

则根据Riccati方程求出P，在求出K，从而可以得出下一步的控制量。

LQR from wikipedia

无穷时域连续时间 Finite-horizon， continuous-time
有穷时域连续时间 Finite-horizon, continuous-time
无穷时域离散时间 Finite-horizon， continuous-time
有穷时域离散时间 Finite-horizon, continuous-time

$u[k]=-K[k]X[k] \\$

离散时间序列上通过动态规划的方式，从后向前递推控制量。

iLQR / DDP

LQR中的A和B是常量，适用于现行系统，但是对于非线性系统，A和B是一个变化的量。iLQR就是针对非线性系统在局部进行线性化。先采取初始的控制量走一遍得到初始轨迹。在初始轨迹上作为参考点进行线性化，在采用LQR的方法求出最优控制量。

给定一条轨迹， DDP在此基础上的出更优的策略和轨迹

# Riccati differential equation solver

import scipy.linalg as sp_linalg
sp_linalg.solve_continuous_are(A, B, Q, R)
sp_linalg.solve_discrete_are(A, B, Q, R)

贝尔曼原理

动态规划：多阶段决策。对环境完全已知，即知道状态转移概率和reward

principle of optimality: 最优性原则

预测问题

控制问题

LQR的动态规划角度

ref cs294 有限时域

假设状态方程：

$x_{t+1}=A_tx_t+B_tu_t$

二次代价函数

$J= \sum _ {t=0}^ {H-1} ( x_ {t}^ {r} Q_ {t} x_ {t} + u_ {t}^ {r} R_ {t} u_ {t} )+ x_ {H}^ {r} P_ {H} x_ {H}$

优化目标：

$\begin{aligned} & \min_{u_0 ... u_{H-1}} J \\ &= \min_{u_0 ... u_{H-1}} \sum_{t=0}^{H-1} (x_t^T Q_t x_t + u_t^T R_t u_t) + x_H^T P_H x_H \\ &= \min_{u_0 ... u_{H-2}} \sum_{t=0}^{H-2} (x_t^T Q_t x_t + u_t^T R_t u_t) + x_{H-1}^T Q_{H-1} x_{H-1} + \min_{u_{H-1}} u_{H-1}^T R_{H-1} u_{H-1} + x_H^T Q_H x_H \end{aligned}$

首先考虑优化 $u_{H-1}$ , 并根据状态方程替换条 $x_H$ :

$\begin{aligned}& u_{H-1}^T R_{H-1} u_{H-1} + x_H^T Q_H x_H \\ &= u_{H-1}^T R_{H-1} u_{H-1} \\ & + (A_{H-1} x_{H-1} + B_{H-1} u_{H-1})^T Q_H (A_{H-1} x_{H-1} + B_{H-1} u_{H-1})\end{aligned}$

上式是关于 $u_{H-1}$ 的凸二次函数，令其导数为0可以找到最小值：

$\begin{aligned} \nabla_{u_{H-1}}(\cdot) &= 0 \\ &= 2 R_{H-1} u_{H-1} + 2 B_{H-1}^T Q_H A_{H-1} x_{H-1} + 2 B_{H-1}^T Q_H B_{H-1} u_{H-1} \\ u_{H-1} & = -(R_{H-1} + B_{H-1}^T Q_H B_{H-1})^{-1} B_{H-1}^T Q_H A_{H-1} x_{H-1} \\ & = K_{H-1} x_{H-1} \\ K_{H-1} &= -(R_{H-1} + B_{H-1}^T Q_H B_{H-1})^{-1} B_{H-1}^T Q_H A_{H-1} \end{aligned}$

把 $u_{H-1}$ 的最优值带入原方程消去 $u_{H-1}, x_{H}$ 得：

$\begin{aligned} & \min_{u_0 ... u_{H-1}} J \\ &= \min_{u_0 ... u_{H-1}} \sum_{t=0}^{H-1} (x_t^T Q_t x_t + u_t^T R_t u_t) + x_H^T P_H x_H\\ &= \min_{u_0 ... u_{H-2}} \sum_{t=0}^{H-2} (x_t^T Q_t x_t + u_t^T R_t u_t) + x_{H-1}^T P_{H-1} x_{H-1} \\ P_{H-1} &= Q_{H-1} + K_{H-1}^T R_{H-1} K_{H-1} + (A_{H-1} + B_{H-1} K_{H-1})^T Q_H (A_{H-1} + B_{H-1} K_{H-1}) \end{aligned}$

可以看出这并没有改变原来的问题形式，因此可以通过动态规划的方式递归解决(类似 value i胎儿啊提哦你)：

$\begin{aligned} & \text{for } t = H-1 \text{ to } 0 \\ & \qquad K_t \leftarrow -(R_t + B_t^T P_{t+1} B_t)^{-1} B_t^T P_{t+1} A_t \\ & \qquad P_t \leftarrow Q_t + K_t^T R_t K_t + (A_t + B_t K_t)^T P_{t+1} (A_t + B_t K_t) \\ & \qquad u_t = K_tx_t \\ & \text{next } t \\ \end{aligned}$

总代价： $J(x)=x^TP_0x$ . 这一代价也可以看作从初始状态出发，在最优策略下的将要产生的最小代价。

DDP的动态规划角度

更一般的角度/MDP的角度：状态，动作, $\mu_t: S \rightarrow A$

$min_{\mu_\cdots\mu_{H-1}}\sum_{t=0}^{H-1}g_t(x_t, u_t)+g_H(x_t) \\ x_{t+1}=f(x_t, u_t) \\ u_t=\mu_t(x_t)$

DDP solution:

Set $i = 0$
Run $\pi^{i}$ , record state and input sequence $x_{0}^{i}, u_{0}^{i}, ...$
Compute $A_{t},B_{t},a_{t}$ $\forall t$ linearization about $x_{t}^{i}, u_{t}^{i}$

ie. $x_{t+1} = A_t x_t + B_t u_t + a_t$ (Aside: linearization is a big assumption!)

Compute $Q_{t},q_{t},R_{t},r_{t}$ by quadratic approximation about $x_{t}^{i}, u_{t}^{i}$

$\min_{\mu_1 ... \mu_H} \sum(x_t^{\top} Q_t x_t + aq_{t}^{T} P_H x_t + u_t^{\top} R_t u_t)$
Run LQR, which gives us $\pi^{i+1} : \mu^i_t(x) = K_t(x)+ k_t$

分析：

所谓 $\pi^0$ 就是指初始参考轨迹，也可称为动作策略，即怎么选择控制量
LQR最优的前提是现行系统，二次损失
在线性点的误差肯那个很大
如果Q，R非正定，把负的特征值设为0
避免线性化（自动微分？）
线性化点不要偏离初始轨迹太远
实操中关于更新： $x_{t+1}=\alpha x_t +(1-\alpha) f(x_t, u_t)$

滚动时域DDP（Receding horizon DDP）: 在无限时域上求积分是不现实的，实际中可以设定一定步长变为有限离散个数。

shooting方法中的开环控制:

$\min_{u_),u_1,\cdots,u_H}c(x_0, u_0)+c(f(x_0, u_0), u_1)+c(f(f(x_0, u_0), u_1), u_2), \cdots$

而iLQR可以看成是：Specific example of a shooting method, with linear controllers, and second order optimization

自动驾驶中控制优化方法

mpc

lqr

最优控制角度：

iLQR / DDP

贝尔曼原理

LQR的动态规划角度

DDP的动态规划角度

Cilqr

applications

affine system

ref