parallel parking planner

Continuous-Curvature Path Planning

2013

fresnel integral

wiki

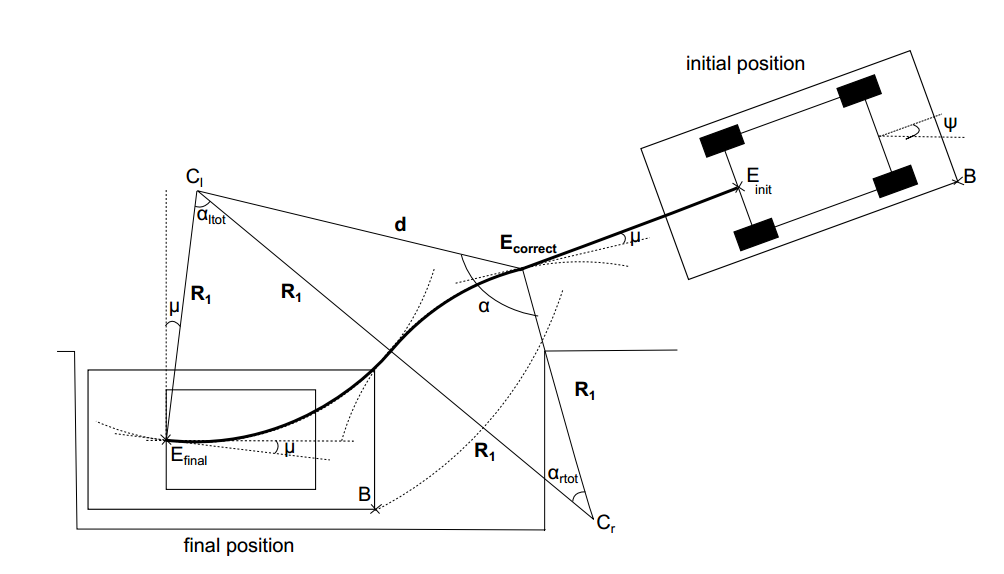
parallel parking in one tria

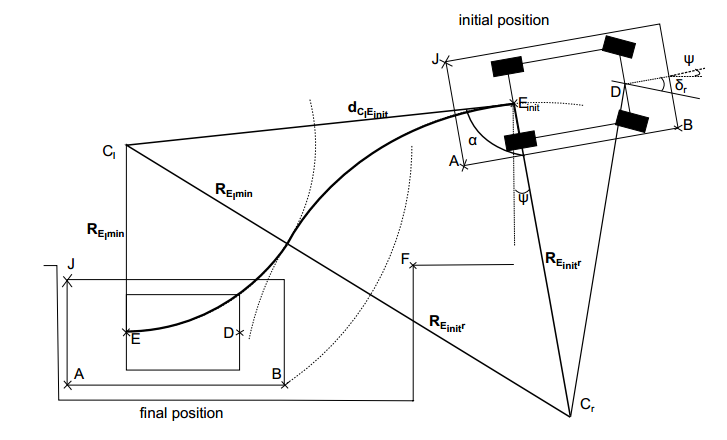
根据余弦订理 $c^2 = a^2 + b^2 -2abcos\theta$

可求出$R_{E_{init^r}}$

$\begin{aligned} R_{E_{i n i t} r} &=\frac{d_{C_{l} E_{\text {init }}}{ }^{2}-R_{E_{l} \min }{ }^{2}}{2 R_{E_{l} \min }+2 d_{E_{\text {init }} C_{l}} \cos \alpha} \\ \delta_{r} &=\arctan \left(a / R_{E_{\text {init }} r}\right) \end{aligned}$

LCC

$3 R_{1}^{2}-d^{2}+2 d R_{1} \cos \alpha=0$

$\left\{\begin{array}{l}d=\sqrt{\left(x_{C l}-x_{E_{\text {correct }}}\right)^{2}+\left(y_{C l}-y_{E_{\text {correct }}}\right)^{2}} \\ \alpha=\arccos \frac{\left|y_{E_{\text {correct }}}-y_{C l}\right|}{d}-\mu+\psi_{E_{\text {init }}} \\ y_{E_{\text {correct }}}=y_{E_{\text {init }}}-\left(x_{E_{\text {init }}}-x_{E_{\text {correct }}}\right) \tan \psi_{E_{\text {init }}}\end{array}\right.$

continuous curvature turn

parametrical clothoid（参数螺旋线）

$\kappa(s)=\kappa_{0}+\alpha s \\ \theta(s)=\int_{0}^{s} \kappa(u) d u \\ x(s)=\int_{0}^{s} \cos \theta(u) d u \\ y(s)=\int_{0}^{s} \sin \theta(u) d u$

$\alpha$: sharpness, rate of curvature
curvature
deflection
length

if $\kappa_0 = 0$, then at end:

$\kappa=\sqrt{2 \delta \alpha}, \delta=\frac{\kappa^{2}}{2 \alpha}, s=\sqrt{\frac{2 \delta}{\alpha}} \\ \delta = \frac{1}{2}\alpha s^2 \\ \theta_{lim} = \alpha s^2$

at middle:

$q = \left\{ \begin{aligned} x&=\sqrt{\frac{\pi}{\alpha}}C_f(\sqrt{\frac{\kappa^2}{\alpha \pi}}) \\ y&=\sqrt{\frac{\pi}{\alpha}}S_f(\sqrt{\frac{\kappa^2}{\alpha \pi}}) \\ \kappa & = \kappa \\ \theta &= \frac{1}{2}\alpha s^2 \end{aligned} \right.$

$\sqrt{\frac{\kappa^2}{\alpha \pi}} = s\sqrt{\frac{\alpha}{\pi}}$

Fresnel integrals:

$C_{f}(x)=\int_{0}^{x} \cos \frac{\pi}{2} u^{2} d u \\ S_{f}(x)=\int_{0}^{x} \sin \frac{\pi}{2} u^{2} d u$

CC curve

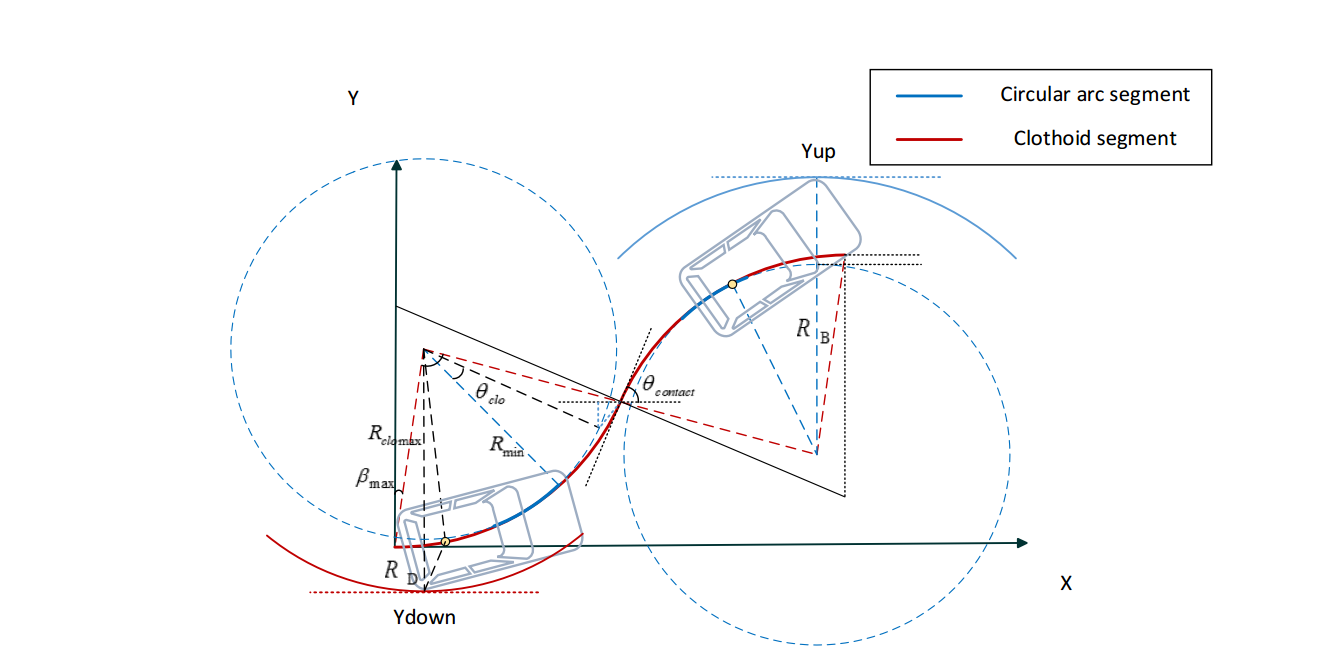
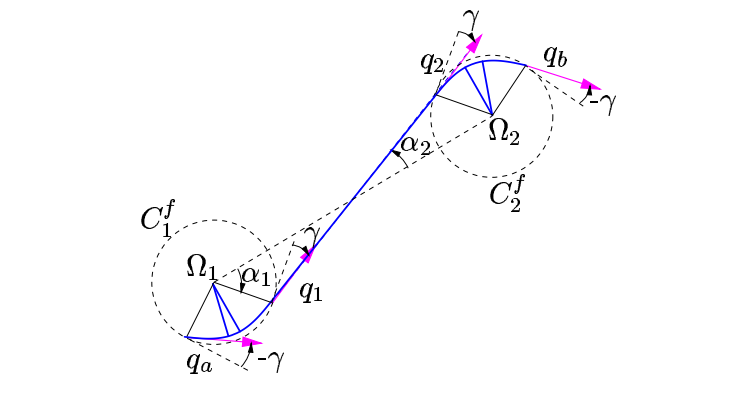
内切圆

$\begin{aligned} R(\theta) &= \frac{x}{\sin \theta} \\ &= \sqrt{\frac{\pi}{\alpha}}C_f(s\sqrt{\frac{\alpha}{\pi}}) / \sin \theta \\ &= \sqrt{\frac{\pi}{\alpha}}C_f(\sqrt{\frac{\theta}{\pi}}) / \sin \theta \end{aligned}$

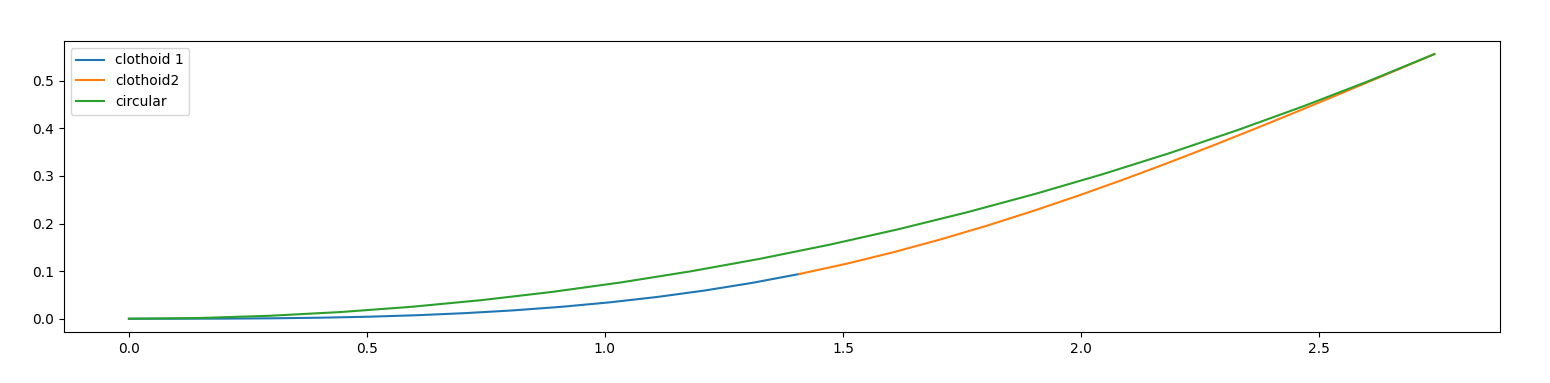
$\theta_{lim}=\frac{\kappa_{max}^{2}}{2 \alpha}$

if $\theta <\theta_{lim}: R(\theta)=R(\theta)$

if $\theta \geq\theta_{lim}: R(\theta)=R(\theta_{lim})$

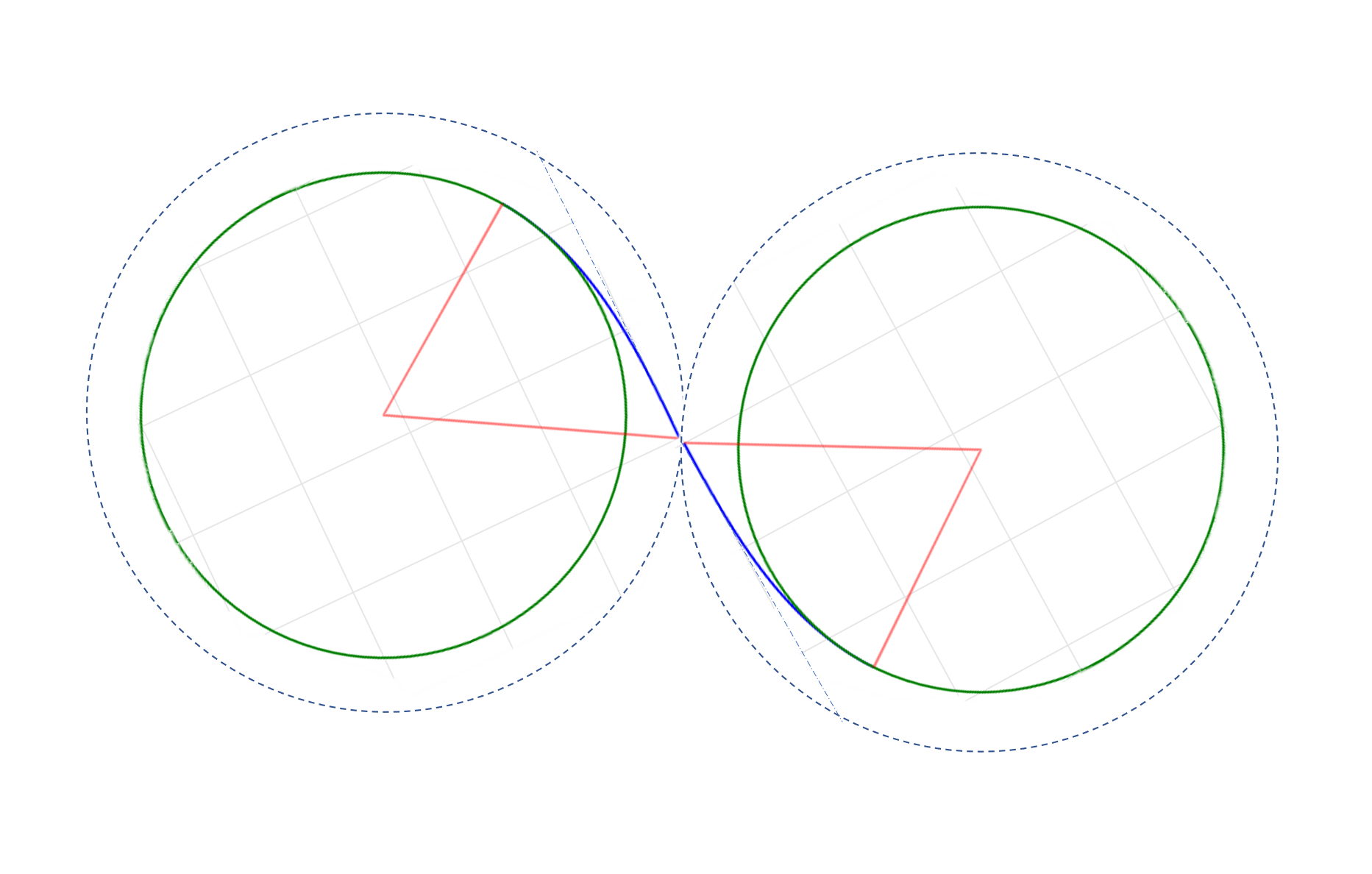
螺旋线与圆相切

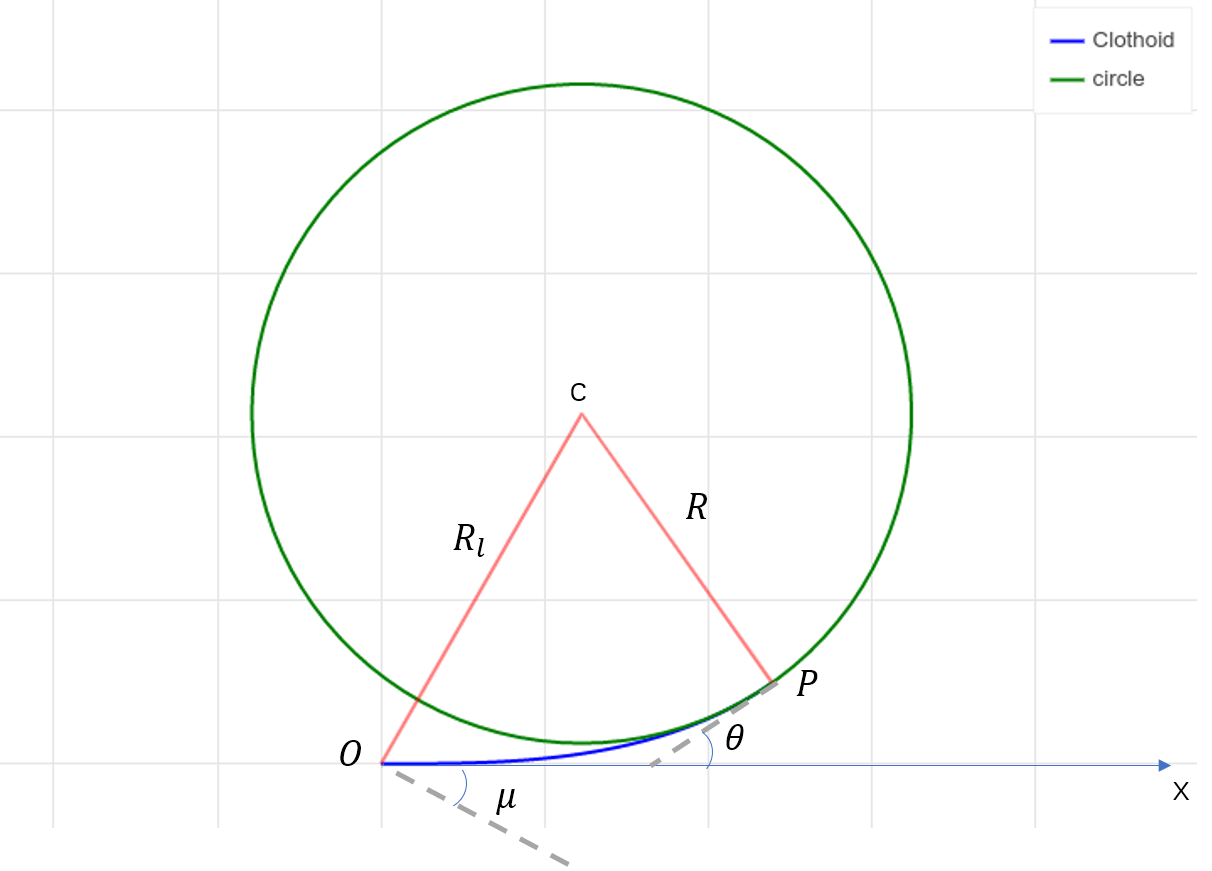
螺旋线与圆相切实际上就是直线过渡到圆的螺旋线路径。

在表达式中$\kappa(s)=\alpha s$，曲率变化率$\alpha$确定之后，则可以通过转弯半径$R$计算出一段从直线过度到圆的螺旋线$C_{OP}$.圆心$c$通过端点$P$的位置以及$\theta$确定。

$P = \left\{ \begin{aligned} \kappa_p &= \frac{1}{R}\\ x_{p}&=\sqrt{\frac{\pi}{\alpha}}C_f(\sqrt{\frac{\kappa_p^2}{\alpha \pi}}) \\ y_{p}&=\sqrt{\frac{\pi}{\alpha}}S_f(\sqrt{\frac{\kappa^2}{\alpha \pi}}) \\ s_p &= \frac{1}{R\alpha} \\ \theta_{p} &= \frac{1}{2}\alpha s^2 = \frac{1}{2}k_ps_p \end{aligned} \right.$

连接圆心$c$和起点$O$可以得到一个更大的半径$R_l$，螺旋线$C_{OP}$就在这个更大的圆内，并且起点$O$与大圆在$O$点的切线夹角记为$\mu$. 可以看出螺旋线$\vec{OP}$的终点斜率和大圆在X轴处的斜率保持一致。

两圆相切的过渡曲线 CPSPC

由上一节可知螺旋线的出圈点在大圆的弦上，弦和切线的夹角为$\mu$。