geometric programming

what is

• geometric programming: 几何规划
• polynomials: [数]多项式（polynomial 的复数形式）
• monomials: 单项式

In the context of geometric programming a monomial is a function from $\mathbb{R}^n_{++}\rightarrow \mathbb{R}$ defined as:

$$g(x) = c x_1^{a_1} x_2^{a_2} ... x_n^{a_n}$$

where $c>0, a_i\in \mathbb{R}$. Such as :

$$7x \qquad 4xy^2z \qquad \frac{2x}{y^2z^{0.3}} \qquad \sqrt{2xy}$$

Building on this, a posynomial is defined as a sum of monomials:

$$f(x) = \sum_{k=1}^K c_k x_1^{a_1k} x_2^{a_2k} ... x_n^{a_nk}$$

Such as:

$$x^2 + 2xy + 1 \qquad 7xy + 0.4(yz)^{-1/3} \qquad 0.56 + \frac{x^{0.7}}{yz}$$

A geometric program (GP) is an optimization problem of the form

$$\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { subject to } & f_i(x) \leq 1, \quad i=1, \ldots, m \\ & g_i(x)=1, \quad i=1, \ldots, p, \end{array}$$

where $f_0, \ldots, f_m$ are posynomials and $g_1, \ldots, g_p$ are monomials. Some GP programming example:

$$\begin{split}\begin{array}{llll}\text{} \text{minimize} & x^{-1}y^{-1/2}z^{-1} + 2.3xz + 4xyz \\ \text{subject to} & (1/3)x^{-2}y^{-2} + (4/3)y^{1/2}z^{-1} \leq 1 \\ & x + 2y + 3z \leq 1 \\ & (1/2)xy = 1 \end{array}\end{split}$$

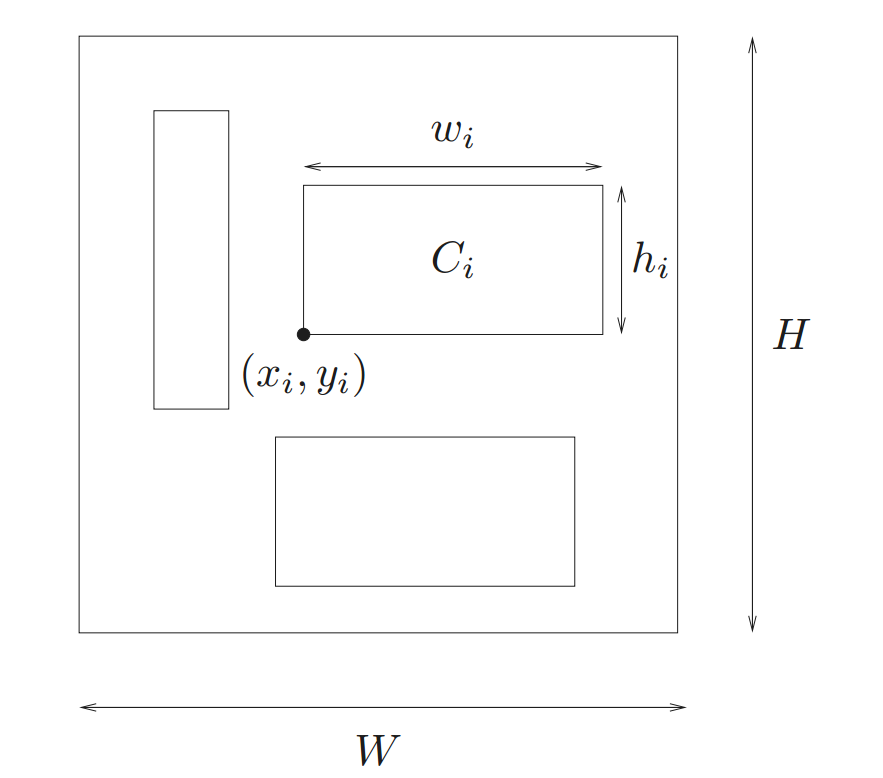
Another example, floor planning:

$$\begin{aligned} \min_{W,H,x,y,w,h } \quad & WH \\\text{subject to} \quad &0\leq x_{i}\leq W,\ i=1,\cdots n\\ &0\leq y_{i}\leq H,\ i=1,\cdots n\\ &x_{i}+w_{i}\leq x_{j},\ (i,j)\in \mathcal{L} \\ & y_{i}+h_{i}\leq y_{j},\ (i,j)\in \mathcal{B} \\ & w_{i}h_{i}=C_{i},\ i=1,\cdots n.\end{aligned}$$

Convex form

Any GP can be made convex by means of a change of variables. Given $g(x) = c x_1^{a_1} x_2^{a_2} ... x_n^{a_n}$, let $y_i = \log x_i$, and rewrite this as:

$$c (e^{y_1})^{a_1} (e^{y_2})^{a_2} ... (e^{y_n})^{a_n} = e^{a^Ty+b}, b = \log c$$

Also, a polynominal can be written as $\sum^p_{k=1} e^{a_k^Ty + b_k}$. With this variable substitution, and after taking logs, a geometric program is equivalent to

$$\begin{aligned} \min_y & \quad \log(\sum^{p_0}_{k=1}e^{a_{0k}^Ty+b_{0k}}) \\ \text{subject to} ~& \quad \log(\sum^{p_i}_{k=1}e^{a_{ik}^Ty+b_{ik}}) \leq 0, i=1, \cdots, m \\ &\quad c^T_{j}y+d_j = 0, j=1,\cdots r \end{aligned}$$

This is convex, recalling the convexity of soft max functions. This log-log transformation can be used to convert a larger class of problems, known as log-log convex programming (LLCP), into an equivalent convex form.

special character:

• Unlike most non-linear optimization problems, large GPs can be solved extremely quickly. If there exists an optimal solution to a GP, it is guaranteed to be globally optimal. Modern GP solvers require no initial guesses or tuning of solver parameters.