12_gradient_decent

梯度下降改进算法

一个高屋建瓴的框架： - 初始化： - 优化参数：$w$ - 目标函数：$f(w)$ - 学习率：$\alpha$ - 迭代 1. 计算目标函数关于当前参数的梯度：$g_t=\nabla f(w_t)$ 2. 根据历史梯度计算一阶动量和二阶动量：$m_{t}=\phi\left(g_{1}, g_{2}, \cdots, g_{t}\right) ; v_{t}=\psi\left(g_{1}, g_{2}, \cdots, g_{t}\right)$ 3. 计算当前时刻的下降梯度：$\eta_{t}=\alpha \cdot m_{t} / \sqrt{v_{t}}$ 4. 根据下降梯度进行更新:$w_{t+1}=w_{t}-\eta_{t}$

为了防止分母为0,通常需要加入平滑项$\epsilon$，一般取1e-8：$\eta_{t}=\alpha \cdot m_{t} / \sqrt{v_{t}+\epsilon}$

SGD optimization on saddle point：

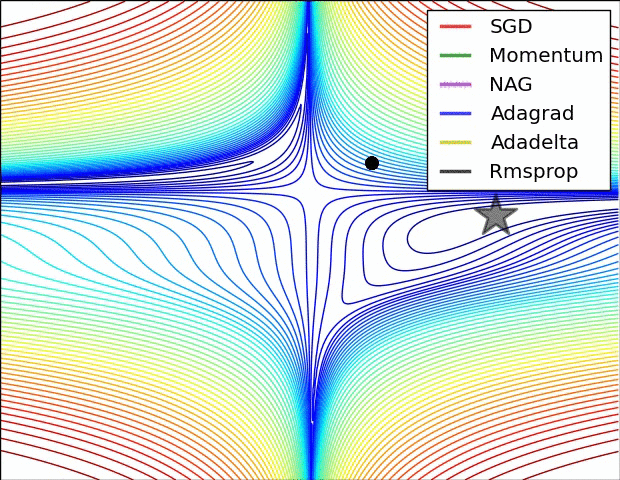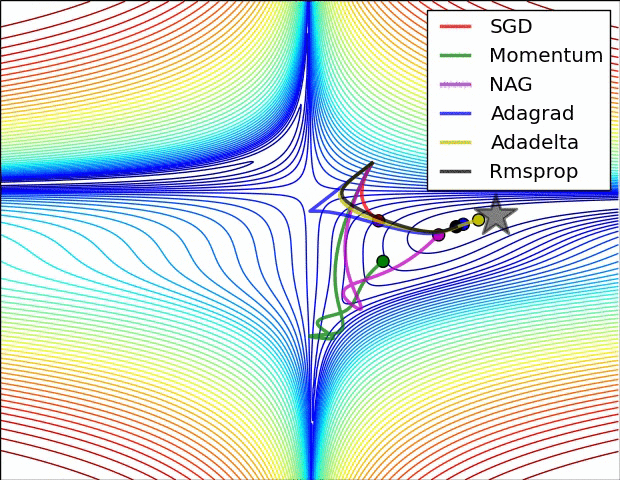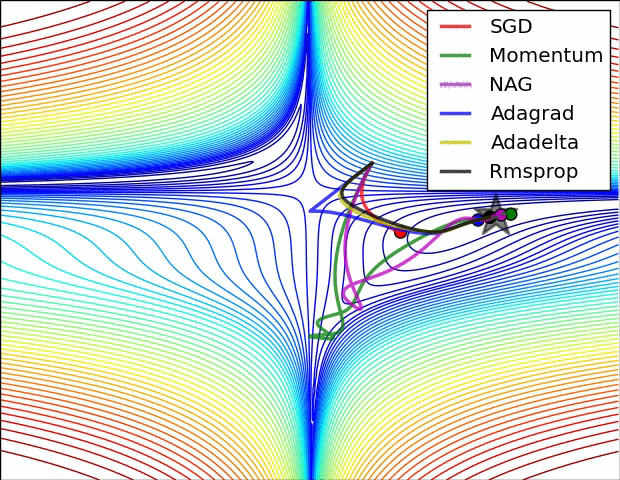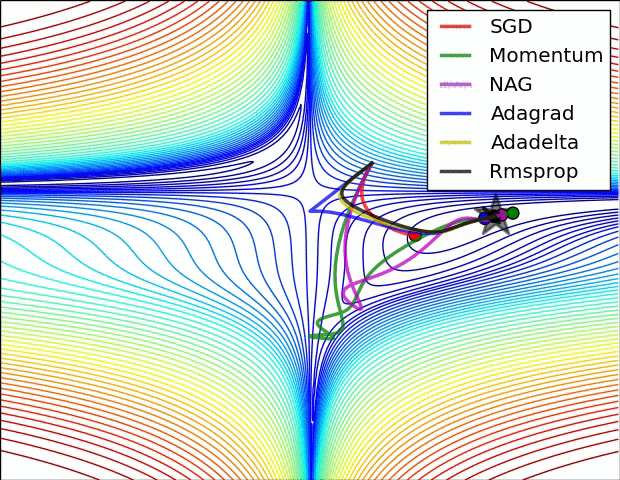
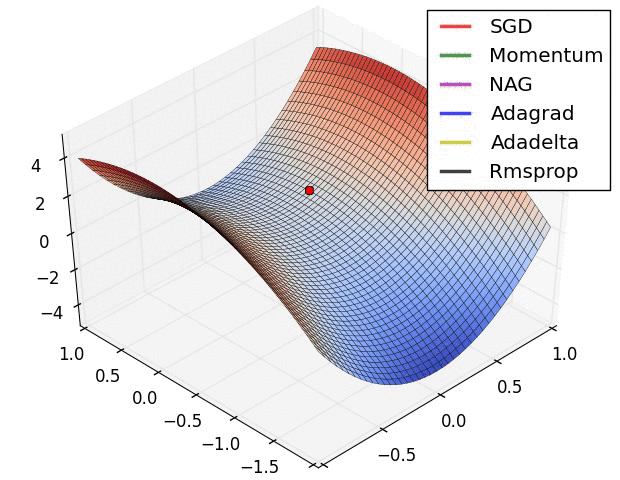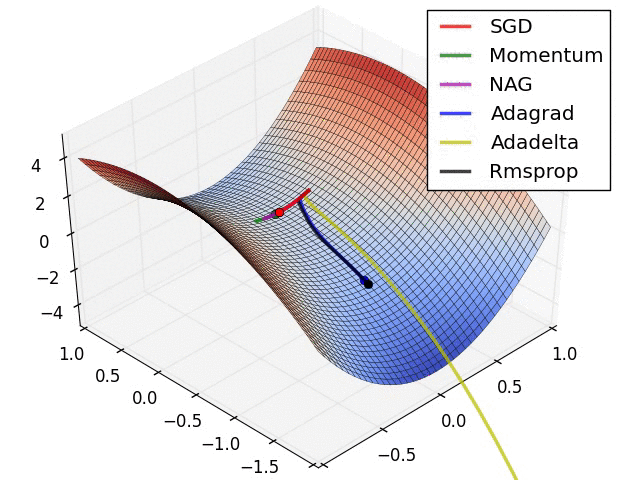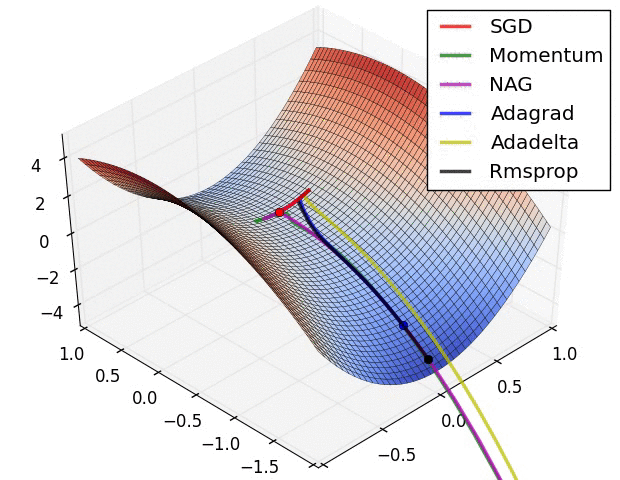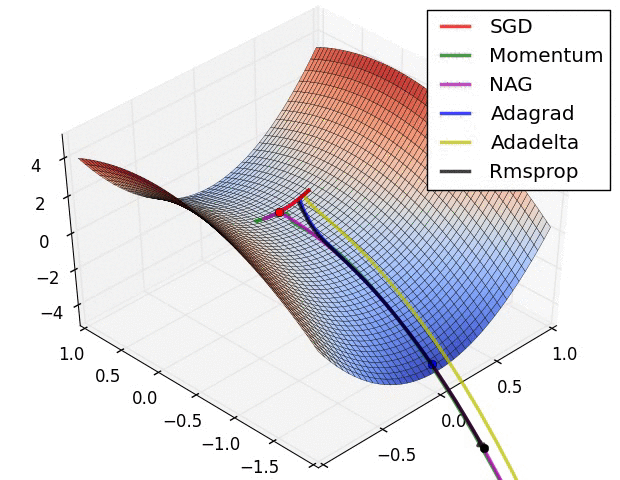
SGD

随机梯度下降SGD: Stochastic Gradient Descent. 没有动量的概念，即 $m_t=g_t \\ v_t=I^2 \\ \eta_t=\alpha\cdot g_t$

缺点： - 下降速度慢 - 可能会在沟壑的两边持续震荡，停留在一个局部最优点

SGDM

SGD with Momentum.在SGD基础上引入了一阶动量,加入惯性: $m_{t}=\beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t} \\ \eta_t=\alpha\cdot m_t$

(也有将一阶动量写作：$m_t=\beta_1m_{t-1}+g_t$)

即下降方向不仅由当前梯度方向决定，还由此前积累的下降方向决定。$\beta_1$的经验值为0.9，这就意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。 - 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的$\beta_1$能够进行很好的加速 - 下降中后期时，在局部最小值来回震荡的时候，$gradient\rightarrow0$，$\beta_1$使得更新幅度增大，跳出陷阱在梯度改变方向的时候，$\beta_1$能够减少更新总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛

NAG

Nesterov Accelerated Gradient. 改进点在步骤1. 即所求梯度不是当前梯度而是计算如果按照上次的累计动量前进一步之后的梯度，即： $g_{t}=\nabla f\left(w_{t}-\alpha \cdot m_{t-1} / \sqrt{v_{t-1}}\right) \\ m_{t}=\beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t} \\ \eta_t=\alpha\cdot m_t$

Nesterov的改进就是让之前的动量直接影响当前的动量。

AdaGrad

二阶动量的出现以及”自适应学习率“优化算法。自适应学习率的要求是：对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。

二阶动量定义为——在该维度上，迄今为止所有梯度值的平方和： $v_t=\sum^t_{\tau=1}g^2_\tau$ 根据步骤3中的下降梯度公式： $\eta_{t}=\alpha \cdot m_{t} / \sqrt{v_{t}}$ 可以看出实质上的学习率由$\alpha$变成$\alpha/\sqrt{v_t}$(为了避免分母为0,加入平滑项$\epsilon$)。而且参数更新越频繁，即梯度的平方累加量越大，即二阶动量越大，则学习率越小。

特点：

前期$\sqrt{v_t}$较小的时候，能够放大梯度
后期$\sqrt{v_t}$较大的时候，能够约束梯度
适合处理稀疏梯度

缺点： - 由公式可以看出，仍依赖于人工设置一个全局学习率 - 全局学习率设置过大的话，会使二阶动量过于敏感，对梯度的调节太大 - 中后期，分母上梯度平方的累加将会越来越大，使得学习率递减至0，使得训练提前结束，无法学习到后续的数据

AdaDelta

不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。 $v_{t}=\beta_{2} * v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2}$

进一步使用梯度期望： $E\left|g^{2}\right|_{t}=\rho * E\left|g^{2}\right|_{t-1}+(1-\rho) * g_{t}^{2}\\ \eta_{t}=\frac{\sum^{t-1}_{r=1}\Delta x_r}{\sqrt{E|g^2|_t+\epsilon}}$

此时，可以看出Adadelta已经不用依赖于全局学习率了。

特点： - 训练初中期，加速效果不错，很快 - 训练后期，反复在局部最小值附近抖动

RMSprop

RMSprop与AdaDelta类似，对期望求根可以得到均方根： $RMS|g|_t=\sqrt{E|g^2|_t+\epsilon}\\ \eta_{t}=\frac{\alpha}{RMS|g|_t}*g_t$

特点： - 适合处理非平稳目标 - 对于RNN效果很好

Adam

Adaptive Moment Estimation,把一阶动量和二阶动量联合起来。

$m_{t}=\beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t} \\ v_{t}=\beta_{2} * v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2} \\ \eta_{t}=\alpha \cdot m_{t} / \sqrt{v_{t}}$

两个超参数$\beta_1,\beta_2$

Nadam

在Adam的基础上增加Nesterov项: Nesterov + Adam = Nadam $g_{t}=\nabla f\left(w_{t}-\alpha \cdot m_{t-1} / \sqrt{v_{t-1}}\right)$

12_gradient_decent_variants