12_gradient_decent

$$x^+ = x - t \nabla f(x)$$

梯度下降步长的选择至关重要，不能太大或者太小。line search是线性搜索步长的一大类方法的统称。

Backtracking line search：

Backtrack: 回溯

要求： 目标函数要求可微并显式知道梯度函数

1. select parameters $0<\beta < 1$ and $0< \alpha \leq 1/2$
2. at each iteration, start with $t=1$, and while:

$$f(x-t\nabla f(x))> f(x) - \alpha t||\nabla f(x)||^2_2$$

shrink $t = \beta t$, Else perform gradient descent update:

$$x^+ = x - t\nabla f(x)$$

解释：对于当前点$x_i$,不同的$t$会产生不同的$f(x_i-t\nabla f(x_i))$，$f(x_i-t\nabla f(x_i))$在局部情况下会按照所期望的慢慢减小，但是如果$t$过大$f(x_i-t\nabla f(x_i))$不会减小很多，甚至会上升.知觉告诉我们在大部分情况下 $f(x_i-t\nabla f(x_i))$ 会是如下图实线所表示的一样是先下降后上升的趋势。为了近可能的降低$f$，希望当减小的较小的时候能或者是当步长越过最低值之后能减小$t$以减小步长。该方法的做法是对当前的切线 $f(x) - t||\nabla f(x)||^2_2$，标记为$l_1$放宽到$\alpha$倍，即$f(x) - \alpha t||\nabla f(x)||^2_2$，标记为$l_2$.$\alpha \in(0, 0.5)$，因此放宽之后的线会更加平缓。该方法对迭代步长之后的值进行了一下比较，如果迭代之后仍然在$l_2$上方，说明迭代的步长可能过长(?)，以至于迈过了最优值，需要减小步长。

疑问点： 如果迭代之后仍然在$l_2$上方，也有可能是步长太短了，怎么能保证有效性？

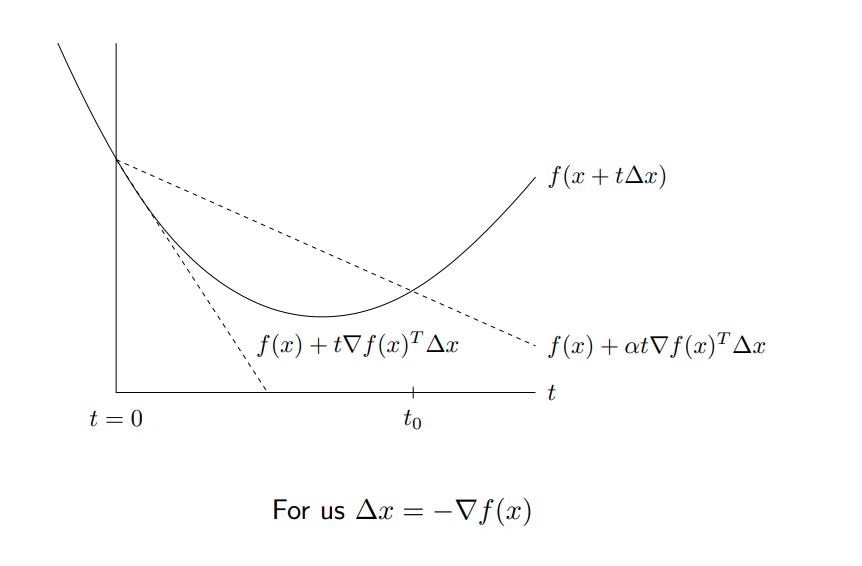
Armijo–Goldstein condition

校验以一定步长更新以后函数值是否能有效地收敛，防止较大的步长收敛速度较慢。如下图所示，l1是沿当前梯度的更新变化趋势， 是f的一个近似，步长约大约不准确。更新的原则希望f能够下降的较快，因此以l2做限制。由于$\alpha \in (0, 1/2)$， l2总是在l1上方。因此若f在l2上方，则说明f的下降趋势较慢，步长太大了需要缩小使得f落入l2一下。

• $\alpha \in (0, 1/2)$
• $d_k$: raw step
• $t d_k$: real step

$$f(x+t d_k)\leq f(x) + t \alpha \nabla f(x)^T d_k$$

Wolfe-Powell condition

$$f(x+t d_k)\leq f(x) + t \alpha \nabla f(x)^T d_k \\ \nabla f(x_k + t d_k)^T d_k \geq \alpha \nabla f(x_k)$$

使得更新点处的斜率减小

exact line search

choose step to do the best we can along direction of negative gradient.

$$t = \min_{s\geq 0} \quad f(x-s\nabla f(x))$$

Usually not possible to do this minimization exactly.

Convergence analysis

Assume that $f$ convex and differential, with $dom(f) = \mathbb{R}^n$, and additionally

$$||\nabla f(x)-\nabla f(y)||_2\leq L||x-y||_2$$

I.e, $\nabla f$ is Lipschitz continuous with constant $L>0$.

Convergence analysis for gradient descent

Theorem: Gradient descent with fixed step size $t\leq 1/L$ satisfies:

$$f\left(x^{(k)}\right)-f^{\star} \leq \frac{\left\|x^{(0)}-x^{\star}\right\|_2^2}{2 t k}$$

We say gradient descent has convergence rate $O(1/k)$,i.e to get $f(x^k) - f^* \leq \epsilon$, we need $O(1/\epsilon)$ iterations

Proof:

• $\nabla f$ Lipschitz with constant $L \Rightarrow$ $$f(y) \leq f(x)+\nabla f(x)^T(y-x)+\frac{L}{2}\|y-x\|_2^2 \quad \text { all } x, y$$
• Plugging in $y=x^{+}=x-t \nabla f(x)$, $$f\left(x^{+}\right) \leq f(x)-\left(1-\frac{L t}{2}\right) t\|\nabla f(x)\|_2^2$$
• Taking $0<t \leq 1 / L$, and using convexity of $f$, $$\begin{aligned} f\left(x^{+}\right) & \leq f^{\star}+\nabla f(x)^T\left(x-x^{\star}\right)-\frac{t}{2}\|\nabla f(x)\|_2^2 \\ & =f^{\star}+\frac{1}{2 t}\left(\left\|x-x^{\star}\right\|_2^2-\left\|x^{+}-x^{\star}\right\|_2^2\right) \end{aligned}$$
• Summing over iterations: $$\begin{aligned} \sum_{i=1}^k\left(f\left(x^{(i)}\right)-f^{\star}\right) & \leq \frac{1}{2 t}\left(\left\|x^{(0)}-x^{\star}\right\|_2^2-\left\|x^{(k)}-x^{\star}\right\|_2^2\right) \\ & \leq \frac{1}{2 t}\left\|x^{(0)}-x^{\star}\right\|_2^2 \end{aligned}$$
• Since $f\left(x^{(k)}\right)$ is nonincreasing, $$f\left(x^{(k)}\right)-f^{\star} \leq \frac{1}{k} \sum_{i=1}^k\left(f\left(x^{(i)}\right)-f^{\star}\right) \leq \frac{\left\|x^{(0)}-x^{\star}\right\|_2^2}{2 t k}$$

Convergence analysis for backtracking

Theorem: Gradient descent with backtracking line search satisfies:

$$f\left(x^{(k)}\right)-f^{\star} \leq \frac{\left\|x^{(0)}-x^{\star}\right\|_2^2}{2 t_{min} k}$$

where $t_{min} = \min {1,\beta/L}$

if $\beta$ is not too small, then we dont lose much compared to fixed step size $(\beta/L \quad \text{vs}\quad 1/L)$

Convergence analysis under strong convexity

strong convexity: $f-\frac{m}{2}||x||^2_2$ is convex for some $m>0$. If $f$ is twice differentiable , then this implies

$$\nabla^2 f(x)\succeq mI, \forall x$$

Sharper lower bound than that from usual convexity:

$$f(y)\geq f(x)+\nabla f(x)^T(y-x) + \frac{m}{2}||y-x||^2_2,\forall x,y$$

Theorem: Gradient descent with fixed step size $t\leq 2/(m+L)$ satisfies:

$$f\left(x^{(k)}\right)-f^{\star} \leq c^k\frac{L}{2}||x^{(0)}-x^{\star}||_2^2, 0<c<1$$

• rate with strong convexity is $O(c^k)$, exponentially fast
• to get $f(x^k) - f^* \leq \epsilon$, we need $O(1/\epsilon)$ iterations

Practice at the condition

A look at the conditions for a simple problem，$f(\beta) = \frac{1}{2}||y-X\beta||_2^2$

Lipschitz continuity of $\nabla f$: - This means $\nabla^2f(x)\preceq LI$ - As $\nabla^2f(\beta) = X^TX$, we have $L = \sigma^2_{max}(X)$

Strong convexity of $f$ : - This means $\nabla^2 f(x) \succeq m I$ - As $\nabla^2 f(\beta)=X^T X$, we have $m=\sigma_{\min }^2(X)$ - If $X$ is wide-i.e., $X$ is $n \times p$ with $p>n$-then $\sigma_{\min }(X)=0$, and $f$ can't be strongly convex - Even if $\sigma_{\min }(X)>0$, can have a very large condition number $L / m=\sigma_{\max }(X) / \sigma_{\min }(X)$

A function $f$ having Lipschitz gradient and being strongly convex satisfies: $$m I \preceq \nabla^2 f(x) \preceq L I \text { for all } x \in \mathbb{R}^n,$$ for constants $L>m>0$ Think of $f$ being sandwiched between two quadratics May seem like a strong condition to hold globally (for all $x \in \mathbb{R}^n$ ). But a careful look at the proofs shows that we only need Lipschitz gradients/strong convexity over the sublevel set $$S=\left\{x: f(x) \leq f\left(x^{(0)}\right)\right\}$$ This is less restrictive.

Practicalities

Stopping rules:

stop when $||\nabla f(x)||_2$ is small

• recall $\nabla f(x^) = 0$ at solution $x^$
• if $f$ is strongly convex with parameter $m$, then:

$$||\nabla f(x)||_2\leq \sqrt{2m\epsilon} \Rightarrow f(x) - f^* \leq \epsilon$$

Forward stagewise regression

Steepest descent

Gradient boosting

不是更新函数的参数而是更新函数本身。如果有误差则添加一个新的函数