二次规划

quadratic programming

二次规划的基本形式：

$$\begin{aligned} &\min f(x)=q^T x+\frac{1}{2} x^T Q x \\ &\text { s.t.Ax }=a \\ &B x \leq b \\ &x \geq 0 \end{aligned}$$

$Q$ 可被认为是目标函数的Hessian matrix.

几何视角

• quadratic forms

• geometry of the curves of the contour lines of f(x)=12xtAx+btx+c

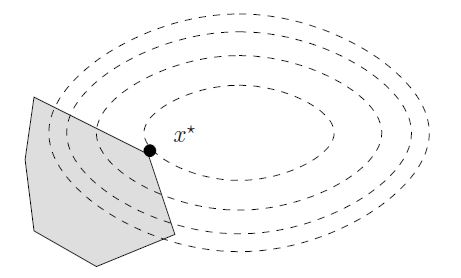
• 相比线性规划，QP的变化是二次引入的等高线(contour line)不再是直线， 这样最优解不再限制在角上，可能是边上或者内部。

ref

1. 另一个则是非凸情况的产生。凸函数对应的是正定矩阵，非凸对应的是不定矩阵（indefinite）

正定矩阵对应的等高线为椭圆。不定矩阵对应的为双曲线。

.png

常用求解方法：

1. 内点法 interior point
2. 激活集法 active set
3. 共轭梯度法 conjugate gradient
4. 椭球法 若Q为正定矩阵，则相应的二次规划问题可由椭球法在多项式时间内求解
5. 增广拉格朗日法 augmented lagrangian
6. 梯度投影法 gradient projection

参数特性

1. 如果Q是半正定矩阵，那么f(x)是一个凸函数。相应的二次规划为凸二次规划问题；此时若约束条件定义的可行域不为空，且目标函数在此可行域有下界，则该问题有全局最小值。
2. 如果Q是正定矩阵，则该问题有唯一的全局最小值。
3. 若Q为非正定矩阵，则目标函数是有多个平稳点和局部极小点的NP问题。
4. 如果Q=0，二次规划问题就变成线性规划问题

目标函数和约束条件：

1. Q是不是半正定的
2. 是只有等式约束还是有不等式约束

无约束条件

求极值

$$\begin{aligned} \nabla f &= Qx+q = 0 \\ x&=Q^{-1}\cdot -q \end{aligned}$$

等式约束

• 消元法
• 拉格朗日乘子法

KKT conditions

拉格朗日函数： $$\begin{aligned} F(X, \lambda, \mu) = f(x) + \lambda^T (Ax-a)+\mu^T (Bx-b) \end{aligned}$$ KKT 条件： $$\begin{aligned} \nabla_x F(X, \lambda, \mu) &= q + Qx + A^T\lambda+B^T\mu \\ Ax -a & = 0 \\ Bx - b & \leq 0 \\ \lambda^T \neq 0,& \quad \mu^T \geq 0, \quad x \geq 0 \end{aligned}$$

等式约束

kkt条件可以写为： $$\begin{bmatrix} Q & A^T \\ A & 0 \end{bmatrix} \begin{bmatrix} x \\ \lambda \end{bmatrix} =\begin{bmatrix} -q \\ a \end{bmatrix}$$

求解变成了解线性方程，在参数规模不大的时候，可以通过矩阵分解求得 $x, \lambda$.

solution strategy

• only equality constraints: conjugate gradient method:
• inequality constraints: interior point and active set methods
• box constraint $x^L\leq x \leq x^U$: trust-region methods
• all general constraint: NLP solver

对偶性

ref

• blog
  • Quadratic_programming
  • 一步一步走向锥规划 - QP
• pdf / book / notes
  • Chapter3