CHMOP planner

CHMOP: Covariant Hamiltonian Optimization for Motion Planning

introduction

轨迹优化在最优控制问题上已能得出最优的结果，而受限于计算资源和局部极值，这一方法很少在运动规划上有类似的成果。而本方法致力于在综合考虑动力学，平滑性和避障的基础上产生最优的运动规划结果。

基于以下两个原则：

1. Gradient information is often available and can be computed inexpensively.
2. Trajectory optimization should be invariant to parametrization

突破限制：

1. 使用蒙特卡罗(Hamiltonian Monte Carlo, HMC) 进行采样，同时产生扰动避免局部极值
2. 运动学约束可以被加入到约束流形中，加速迭代

自身局限：

• 不适于高维运动规划

objective functional

1. smooth gradient

$$\nabla_{\text {smooth }}=\mathbf{A} \xi+\mathbf{b}$$

1. obstacle gradient

$$\nabla_{o b s}(\xi)_i=-W_i \frac{\partial}{\partial \xi_i}\left(\sum_{j=1}^m h\left(d_j(\xi)\right)\right)$$

1. update trajectory

$$\xi \leftarrow \xi-\frac{1}{\eta} \mathbf{A}^{-1}\left(\lambda \nabla_{\text {smooth }}+\nabla_{o b s}\right)$$

障碍物梯度信息：

• integrate across time: moving more quickly through regions of high cost will be penalized less（在时间上积分并不理想，因为如果该点处移动很快，则时间就会很小）
• integrate with respect to an arc-length parameterization: (因此选择根据参数曲线的弧长进行积分，计算代价时考虑的是路径本身的长度，而不是机器人在路径上的速度或花费的时间。使用弧长参数化后，目标函数就不会受速度变化的影响，只和路径的形状有关。通过这种方式，无论机器人沿路径移动的快慢如何改变，都不会影响到总的路径长度和因而产生的总代价？根据这个直观的理解，（functional gradient）的表现形式是将工作空间梯度投影到与运动方向垂直的二维平面上。 这里所说的“投影”意味着我们只考虑那些直接指向提高路径效率（减少代价）的方向的梯度成分。)

$$\mathcal{U}[\xi]=\mathcal{F}_{\text {obs }}[\xi]+\lambda \mathcal{F}_{\text {smooth }}[\xi]$$

• $\xi$： 运动轨迹，机器人构形相对时间的函数。$\xi(0)=q_0, \xi(1)=q_1$
• $\mathcal{F}_{\text {obs }}[\xi]$: 环境障碍物惩罚函数
• $\mathcal{F}_{\text {smooth }}[\xi]$: 动力学平滑惩罚函数

$$\mathcal{F}_{o b s}[\xi]=\int_{0}^{1} \int_{\mathcal{B}} c(x(\xi(t), u))\left\|\frac{d}{d t} x(\xi(t), u)\right\| d u d t$$

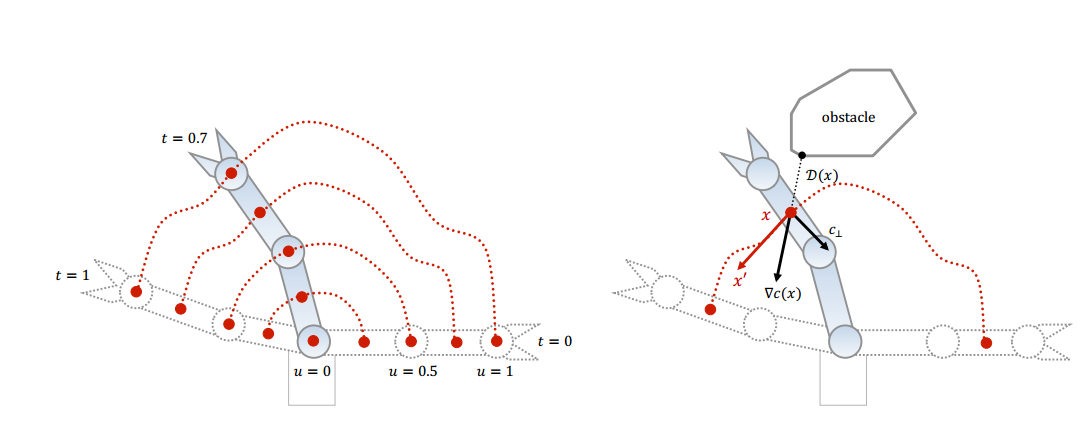
• $x(\xi(t), u)$: 由轨迹点和机器人局部任一位置(body point)定义的全局位置点(workspace position)
• $x'$: 全局位置点的速度
• $\nabla c(x)$: collision cost 的梯度

障碍物惩罚函数定义为对机器人上每一个点的colliison cost在空间和时间上的积分。

$$\mathcal{F}_{o b s}[\xi]=\int_{0}^{1} \max _{u \in \mathcal{B}} c(x(\xi(t), u))\left\|\frac{d}{d t} x(\xi(t), u)\right\| d t$$

为简化计算，在每一时刻只计算最大cost的点。

$$\mathcal{F}_{\text {smooth }}[\xi]=\frac{1}{2} \int_{0}^{1}\left\|\frac{d}{d t} \xi(t)\right\|^{2} d t$$

平滑性以加速度衡量。

functional gradient: 泛函梯度

$$\bar{\nabla} u[\xi]=\frac{\partial v}{\partial \xi}-\frac{d}{d t} \frac{\partial v}{\partial \xi^{\prime}}$$

梯度下降：

$$\xi_{i+1}=\xi_{i}-\eta_{i} \bar{\nabla} U[\xi]$$

pseudocode

smooth_cost_i = (p[i+1] - p[i] + p[i-1] ) / (dt * dt)

// cost 是一个数值
//  grad 表明了方向
if d < 0:
    obs_grad = -gradient
    obs_cost = -d + thres_/2.0
else if d < thres_:
    obs_cost = (d - thres_)^2 / (2*thres_)
    obs_grad = (d - thres_)/thres_ * gradient

x_dt:   (p[i+1] - p[i-1]) / (2 * dt) // velocity
x_dt_dt: (p[i+1] - 2 * p[i] + p[i-1]) / (dt * dt) // acceleration
x_dt_normalized = x_dt / norm(x_dt)
x_dt_prj = I - xd_normalized * x_dt_normalized.T
k = x_dt_prj * x_dt_dt / (norm(x_dt) * norm(x_dt))  // a_perp = k v^2

obs_cost_f = norm(x_dt) * ((x_dt_prj*obs_grad) - obs_cost * k)

Moveit Implementation

chmop in moveit

ChompPlanner::solve(planning_scene, req, params, res)
    // initialize trajectory
    ChompTrajectory trajectory(planning_scene->getRobotModel(), 3.0, .03, req.group_name);

    // fill in start point
    robotStateToArray(start_state, req.group_name, trajectory.getTrajectoryPoint(0));

    // fill in goal point
    robotStateToArray(goal_state, req.group_name, trajectory.getTrajectoryPoint(goal_index));

    // fill in whole trajectory
    // 1. 根据已知轨迹填充
    trajectory.fillInFromTrajectory(*res.trajectory_[0])
    // 2. 曲线拟合方式填充
    trajectory.fillInMinJerk(); // default
    trajectory.fillInLinearInterpolation();
    trajectory.fillInCubicInterpolation();

    // optimization
    optimizer =ChompOptimizer(&trajectory, planning_scene,req.group_name, &params_nonconst, start_state);
    optimizer->optimize();\

ChompOptimizer::
    optimize():
        for i in iterations:
            calculateSmoothnessIncrements()
            calculateCollisionIncrements()
            calculateTotalIncrements()  
            addIncrementsToTrajectory() // 更新轨迹
    getSmoothnessCost():
    getCollisionCost()
    performForwardKinematics()

chomp 中依赖planningscene中的检测器。planningscene默认检测器为CollisionDetectorAllocatorFCL，chomp要求为CollisionDetectorAllocatorHybrid.

ref: CollisionDetectorAllocator

// planning_scene

// 默认情况会自定义一个
setActiveCollisionDetector(collision_detection::CollisionDetectorAllocatorFCL::create());

// 该函数也可以手动调用，设置完之后，该collision会作为最新的检测器
setActiveCollisionDetector()

// 手动设置
planning_scene::PlanningScenePtr ps = planning_scene_->diff();
ps->setActiveCollisionDetector(collision_detection::CollisionDetectorAllocatorHybrid::create(), true);

Trychomp

qs = np.array([-5.0, -5.0])  # 起始点
qe = np.array([7.0, 7.0])    # 结束点

# 初始化轨迹 xi
xi = np.tile(qs, (nq, 1)).flatten()

# 初始化 A, b 和 A_inv
AA = np.zeros((xidim, xidim))
for ii in range(nq):
    AA[ii*cdim:(ii+1)*cdim, ii*cdim:(ii+1)*cdim] = 2.0 * np.eye(cdim)
    if ii > 0:
        AA[ii*cdim:(ii+1)*cdim, (ii-1)*cdim:ii*cdim] = -1.0 * np.eye(cdim)
        AA[(ii-1)*cdim:ii*cdim, ii*cdim:(ii+1)*cdim] = -1.0 * np.eye(cdim)
AA /= dt * dt * (nq + 1)

bb = np.zeros(xidim)
bb[:cdim] = qs
bb[-cdim:] = qe
bb /= - dt * dt * (nq + 1)

Ainv = np.linalg.inv(AA)

在这段代码中，AA和bb都是与轨迹优化相关的矩阵和向量，用于定义一个二次规划问题以生成平滑的轨迹。下面是这两个变量的大小和含义：

AA (矩阵的大小)

AA是一个大小为xidim x xidim的矩阵，其中xidim表示轨迹的总维度，计算方式是轨迹中的点数（nq）乘以配置空间的维度（cdim）。如果按照给定的参数：

• 轨迹中的点数 (nq) = 20
• 配置空间的维度 (cdim) = 2

那么，轨迹的总维度 (xidim) = 20 * 2 = 40。所以，AA是一个40 x 40的矩阵。

AA (矩阵的含义)

AA矩阵代表了轨迹优化问题的二次项系数矩阵，它被用来确保轨迹的平滑性。此矩阵构建了一个离散化的时间加速度代价函数，该函数通过最小化每个时间步长内的加速度变化来生成平滑轨迹。这是通过惩罚相邻轨迹点之间的差异来实现的。

在这段代码中，AA矩阵通过以下操作构建：

• 每个轨迹点对应的二维子矩阵设置为2倍单位矩阵（2.0 * np.eye(cdim)）
• 相邻轨迹点的二维子矩阵之间设置为-1倍单位矩阵（-1.0 * np.eye(cdim)）

这样可以模拟出一种离散的二阶导数（加速度），即每个点处的加速度值由当前点、前一个点和后一个点共同决定。

bb (向量的大小)

bb是一个长度为xidim的向量。同样地，在给定的参数下：

• 轨迹的总维度 (xidim) = 40

因此，bb是一个长度为40的向量。

bb (向量的含义)

bb向量代表了线性项的系数，定义了轨迹优化问题的目标函数中与变量线性相关的部分。在这段代码中，bb向量的前两个元素和最后两个元素分别设置为起始点qs和结束点qe的坐标，其余元素均为0。

这意味着优化问题会考虑到轨迹的起始和结束位置，使得生成的轨迹能够从起始点开始并在结束点结束。

结合AA和bb

结合AA和bb，你可以定义一个二次优化问题，目标是找到一个使得以下代价函数取最小值的轨迹xi：

xi^T * AA * xi + bb^T * xi

其中，xi是代表整条轨迹的向量（包含所有轨迹点的坐标），AA是二次项的系数矩阵，bb是线性项的系数向量。该代价函数旨在使得轨迹尽可能平滑并且能够从指定的起点移动到终点。

bicycle model

方向盘转角

$$\dot{\theta} = v\cdot tan \phi / L \\ \frac{d \theta}{d \phi} = \frac{v}{L}\frac{1}{cos^2 \phi}$$ $$dx/d \phi = \frac{ v\cdot cos\theta}{d \phi} = -v\cdot sin \theta \cdot v\cdot tan \phi / L$$

曲率

$$\dot{\theta} = v\cdot c \\ \frac{d \theta}{d c} = v$$ $$dx = v\cdot cos \theta$$ $$dx/d c = \frac{ v\cdot cos\theta}{d c} = -v\cdot sin \theta \cdot v \\ dy/dc = \frac{ v\cdot sin\theta}{d c} = v\cdot cos \theta \cdot v$$ $$\begin{bmatrix}-s^2\cdot sin\theta & cos \theta \\ s^2sin \theta & sin \theta \\ s & c \end{bmatrix}$$

ref

• blog
• mainpage
  • Optimized Robotics
• relative library
  • trychomp - 2d
  • chomp-multigrid
  • or_cdchomp
  • chomp_planner
  • chomp_planner sdf
  • chomp-multigrid
• paper
  • 2009 ICRA CHOMP: Gradient Optimization Techniques for Efficient Motion Planning
  • 2013 IJRR CHOMP
  • CHOMP: Gradient optimization techniques for efficient motion planning
  • 2014 ICRA T-chomp