轨迹优化之轨迹拟合

2003-Reactive Nonholonomic Trajectory Generation via Parametric Optimal Control

Abstract

parametric trajectory reduce computation time, at the cost os potentially introducing suboptimality

Formulation for a vehicle actuated in curvature and speed:

$\begin{array}{ll} \dot{x}(t)=V(t) \cos \theta(t) & \dot{\theta}(t)=\kappa(t) V(t) \\ \dot{y}(t)=V(t) \sin \theta(t) & { }_{\mathrm{K}}(t)=u(t) \end{array}$

from time to distance(以行驶举例作为参数):

$\begin{aligned} &x(s)=\int_{0}^{s} \cos \theta(s) d s \quad \theta(s)=\int_{0}^{s} \kappa(s) d s \\ &y(s)=\int_{0} \sin \theta(s) d s \quad \kappa(s)=u(s) \end{aligned}$

变分法把最优控制问题转化为非线性优化问题。

solution using polynominal spirals

$\begin{aligned} \kappa(s) &=a+b s+c s^{2}+d s^{3}+\cdots \\ \frac{d}{d s} x(s) &=\cos \theta(s) \\ \frac{d}{d s} y(s) &=\sin \theta(s) \\ \frac{d}{d s} \theta(s)&=\kappa(s) \end{aligned}$

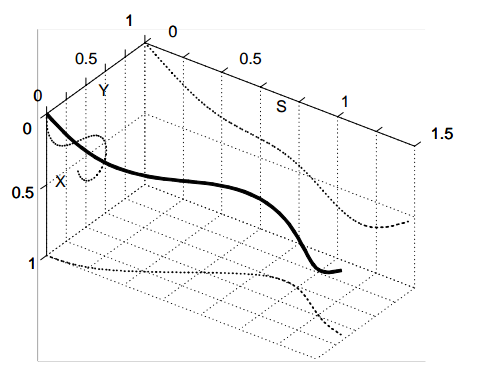
polytraj 代码原理

path：只有路径，以曲率为路径长度的函数
- start($x_s,y_s,\theta_s,\kappa_s$)
- end($x_e,y_e,\theta_e,\kappa_e$)
- 初始化一个曲率多项式: $\kappa(s) =a+b s+c s^{2}+d s^{3}+\cdots$
- 根据动力学约束根据起点求终点, 并最小化终点误差：
$end_state=\int_0^1g(\kappa) \ \min_{s,a,b,\cdots} \quad J=||\Delta e||^2$ - 在代码中使用了Simpson积分公式，首先估计了路径总长度，然后根据路径点均分。 - trajectory：加入了速度和加速度，一条曲线为曲率函数，一条为加速度 - start($x_s,y_s,\theta_s,\kappa_s, v_s, a_s$) - end($x_e,y_e,\theta_e,\kappa_e$)

参数方程/参数曲线/样条曲线：五次样条和三次螺旋线对比

都是参数方程：样条曲线可以选择一个定义域为[0,1]的控制量

quintic splines: 对于二维平面，x和y分别由一个五次样条参数曲线生成，一共有12个参数。在设置完边界条件之后存在封闭解。但是难以对于曲率做控制。

$\begin{gathered} x(u)=\alpha_{5} u^{5}+\alpha_{4} u^{4}+\alpha_{3} u^{3}+\alpha_{2} u^{2}+\alpha_{1} u+\alpha_{0} \\ y(u)=\beta_{5} u^{5}+\beta_{4} u^{4}+\beta_{3} u^{3}+\beta_{2} u^{2}+\beta_{1} u+\beta_{0} \\ u \in[0,1] \end{gathered}$

曲率变化

$\kappa(u)=\frac{x^{\prime}(u) y^{\prime \prime}(u)-y^{\prime}(u) x^{\prime \prime}(u)}{\left(x^{\prime}(u)^{2}+y^{\prime}(u)^{2}\right)^{\frac{3}{2}}}$

Polynomial Spirals：曲率被定义为路径长度的多项式函数，方便对曲率做控制。由于曲率值不会像在五次样条曲线中那样迅速变化。一般通过限制螺旋线和螺旋线中仅几个点的曲率，就很可能满足了整个曲线上的曲率约束。但是由于位置的计算是三角函数的积分形式，难以找出封闭解，因此需要数值逼近。

$\begin{gathered} x(s)=x_{0}+\int_{0}^{s} \cos \left(\theta\left(s^{\prime}\right)\right) d s^{\prime} \\ y(s)=y_{0}+\int_{0}^{s} \sin \left(\theta\left(s^{\prime}\right)\right) d s^{\prime} \\ \int_{0}^{s} f\left(s^{\prime}\right) d s^{\prime} \approx \frac{s}{3 n}\left(f(0)+4 f\left(\frac{s}{n}\right)+2 f\left(\frac{2 s}{n}\right)+\cdots+f(s)\right) \end{gathered}$

曲率约束：除了边界点之外，把线段分成三段，对中间两个点($/frac{1}{3}s, frac{2}{3}s$)作曲率约束。

$|\kappa(\frac{s}{3})|\leq\kappa_{max} \\ |\kappa(\frac{2s}{3})|\leq\kappa_{max}$

parameter remapping

参数重映射：选取三段平分点的曲率和弧长作为五个参数，反解原始曲率曲线参数的a,b,c,d.降低数值迭代的不稳定性

$\begin{array}{cc} k(0)=p 0 & a(p)=p 0 \\ k\left(\frac{s_{G}}{3}\right)=p 1 & b(p)=-\frac{11 p 0-18 p 1+9 p 2-2 p 3}{2 s_{G}} \\ k\left(\frac{2 s_{G}}{3}\right)=p 2 & c(p)=\frac{9(2 p 0-5 p 1+4 p 2-p 3)}{2 s_{G}^{2}} \\ k\left(s_{G}\right)=p 3 & d(p)=-\frac{9(p 0-3 p 1+3 p 2-p 3)}{2 s_{G}^{3}} \end{array}$

轨迹优化之轨迹拟合

2003-Reactive Nonholonomic Trajectory Generation via Parametric Optimal Control

参数方程/参数曲线/样条曲线：五次样条和三次螺旋线对比

parameter remapping

ref