轨迹优化之

轨迹和控制：对单个关节的控制可能无法实现整体的最有优运动。

model based
- Differential Dynamic Programming
- Direct Collocation
- Planning As Interface

legged robots legged locomotion

动力学

非线性系统的线性化

选择泰勒展开的参考点为 $x_{0}, u_{0}$ 对于函数 $f(x, u)$, 在点 $x_{0}, u_{0}$ 处通过一阶泰勒展开获得它的线性化函数为 $f(x, u)=f\left(x_{0}, u_{0}\right)+\left.\frac{\partial f}{\partial x}\right|_{x=x_{0}}\left(x-x_{0}\right)+\left.\frac{\partial f}{\partial u}\right|_{u=u_{0}}\left(u-u_{0}\right)$ 如果我们定义 $x=x_{0}+\delta x$ 和 $u=u_{0}+\delta u$, 则 $\dot{x}=\dot{x}{0}+\delta \dot{x}$,由此可以获得 $\delta \dot{x}=\left.\frac{\partial f}{\partial x}\right|_{x=x_{0}} \delta x+\left.\frac{\partial f}{\partial u}\right|_{u=u_{0}} \delta u$ 如果我们把 $\delta x=x-x\right|}$ 当做我们要研究的状态 $x, \delta u=u-u_{0}$ 为控制量 $u$, 然后令 $A=\left.\frac{\partial f}{\partial x{x=x\right|}}$ 且 $B=\left.\frac{\partial f}{\partial u{u=u$, 则 } $\dot{\delta x}=A \delta x+B \delta u$

二次型调节器

LQR: Linear Quadratic Regulator

如果所研究的系统是线性的，且性能指标为状态变量和控制变量的二次型函数，则最优控制问题称为线性二次型问题。而LQR是指求解线性二次型问题常用的方法。

线性定常连续系统：

$\begin{aligned} &\dot{x}(t)=A x(t)+B u(t) \\ &y(t)=C x(t)+D u(t) \end{aligned}$

一般连续时间系统：

$\begin{aligned} &\dot{x}(t)=f[x(t), u(t), t] \\ &y(t)=g[x(t), u(t), t] \end{aligned}$

线性时变连续系统: $\begin{aligned} &\dot{x}(t)=A(t) x(t)+B(t) u(t) \\ &y(t)=C(t) x(t)+D(t) u(t) \end{aligned}$

令$x$为误差，$w$为误差项系数,令$Q=w_x^Tw_x, R=w_u^Tw_u$为半正定矩阵，也是误差系数.

$J=\int_{0}^{\infty}\left(x^{T} Q x+u^{T} R u\right) d t$

系统稳定时，$u(t)=-Kx(t), \dot{x}(t)=(A-B K) x(t)$,带入代价函数得到:

$\begin{gathered} J=\int_{0}^{\infty}\left(x^{T} Q x+u^{T} R u\right) d t \\ =\int_{0}^{\infty} x^{T}(t)\left(Q+K^{T} R K\right) x(t) d t \end{gathered}$

我们要找到这个积分的原函数, 为了找到 $K$, 假设存在一个常量矩阵 $P$, 使得 $\frac{d}{d t}\left(x(t)^{T} P x(t)\right)=-x^{T}(t)\left(Q+K^{T} R K\right) x(t)$ 对式 $(8)$ 两边取微分 $\dot{x}^{T}(t) P x(t)+x^{T}(t) P \dot{x}(t)+x^{T}(t) Q x(t)+x^{T}(t) K^{T} R K x(t)=0$ 将状态方程代入 $(9):$ $x^{T}(t)\left((A-B K)^{T} P+P(A-B K)+Q+K^{T} R K\right) x(t)=0$ 这个式子要成立的话, 括号里的项必须为恒为零。 $(A-B K)^{T} P+P(A-B K)+Q+K^{T} R K=0$

进一步化简： $A^{T} P+P A+Q+K^{T} R K-K^{T} B^{T} P-P B K=0$ 为了约掉K，取 $K=R^{-1} B^{T} P$, 代入上式得: $A^{T} P+P A+Q-P B R^{-1} B^{T} P=0$

上式为Riccati方程，解得P。最后根据反馈矩阵 $K=R^{-1}B^TP$得到K

选择参数矩阵Q，R
求解Riccati方程得到矩阵P
根据公式计算K

求解

离散化以后的整个问题变成 $\begin{array}{ll} \min _{u} & J=\sum_{n=0}^{T} x[n]^{T} Q x[n]+u[n]^{T} R u[n] \\ \text { s.t. } & x[n+1]=A x[n]+B u[n] \end{array}$ 我们从 $S[N]=Q$ 开始反向求解 Riccati difference equation $S[n-1]=Q+A^{T} S[n] A-A^{T} S[n] B\left(R+B^{T} S[n] B\right)^{-1} B^{T} S[n] A$ 然后每一个时刻的最优控制为 $u[n]^{*}=-R^{-1} B^{T} S[n] x[n]=-K[n] x[n]$

Differential Dynamic Programming

LQR是将状态调节到0,而轨迹跟踪是系统误差为0。

LQR是在 $\delta x \neq 0$，期望通过控制量在一定时间以后使得$\delta x = 0$。另一个类似的问题是反过来，一开始 $\delta x =0$, 期望在一定时间以后使得 $\delta x $为某一常量。

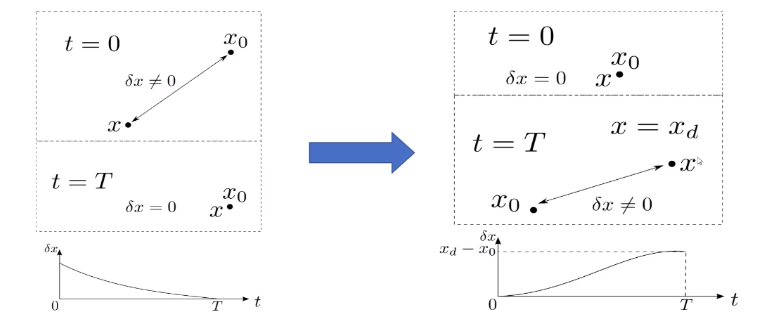
则优化问题变为：

$\begin{array}{ll} \min _{\delta u} & J=\left(\delta x[N]-\delta x_{d}\right)^{T} Q_{f}\left(\delta x[N]-\delta x_{d}\right)+\sum_{n=0}^{N-1} \delta x[n]^{T} Q \delta x[n]+\delta u[n]^{T} R \delta u[n] \\ \text { s.t. } & \delta x[n+1]=A \delta x[n]+B \delta u[n] \\ & \delta x(0)=0 \end{array}$

其中.$\delta x_{d}=x_{d}-x_{0}, Q_{f}$ 是远大于$Q$的正定矩阵. $A，B$在不同的位置需要局部线性化。

lqr 价值函数角度

backward recursion

for $t=T$ to 1 : $\begin{aligned} &\mathbf{Q}_{t}=\mathbf{C}_{t}+\mathbf{F}_{t}^{T} \mathbf{V}_{t+1} \mathbf{F}_{t} \\ &\mathbf{q}_{t}=\mathbf{c}_{t}+\mathbf{F}_{t}^{T} \mathbf{V}_{t+1} \mathbf{f}_{t}+\mathbf{F}_{t}^{T} \mathbf{v}_{t+1} \\ &Q\left(\mathbf{x}_{t}, \mathbf{u}_{t}\right)=\text { const }+\frac{1}{2}\left[\begin{array}{c} \mathbf{x}_{t} \\ \mathbf{u}_{t} \end{array}\right]^{T} \mathbf{Q}_{t}\left[\begin{array}{c} \mathbf{x}_{t} \\ \mathbf{u}_{t} \end{array}\right]+\left[\begin{array}{c} \mathbf{x}_{t} \\ \mathbf{u}_{t} \end{array}\right]^{T} \mathbf{q}_{t} \\ &\mathbf{u}_{t} \leftarrow \arg \min _{\mathbf{u}_{t}} Q\left(\mathbf{x}_{t}, \mathbf{u}_{t}\right)=\mathbf{K}_{t} \mathbf{x}_{t}+\mathbf{k}_{t} \\ &\mathbf{K}_{t}=-\mathbf{Q}_{\mathbf{u}_{t}, \mathbf{u}_{t}}^{-1} \mathbf{Q}_{\mathbf{u}_{t}, \mathbf{x}_{t}} \\ &\mathbf{k}_{t}=-\mathbf{Q}_{\mathbf{u}_{t}, \mathbf{u}_{t}}^{-1} \mathbf{q}_{\mathbf{u}_{t}} \\ &\mathbf{V}_{t}=\mathbf{Q}_{\mathbf{x}_{t}, \mathbf{x}_{t}}+\mathbf{Q}_{\mathbf{x}_{t}, \mathbf{u}_{t}} \mathbf{K}_{t}+\mathbf{K}_{t}^{T} \mathbf{Q}_{\mathbf{u}_{t}, \mathbf{x}_{t}}+\mathbf{K}_{t}^{T} \mathbf{Q}_{\mathbf{u}_{t}, \mathbf{u}_{t}} \mathbf{K}_{t} \\ &\mathbf{v}_{t}=\mathbf{q}_{\mathbf{x}_{t}}+\mathbf{Q}_{\mathbf{x}_{t}, \mathbf{u}_{t}} \mathbf{k}_{t}+\mathbf{K}_{t}^{T} \mathbf{Q}_{\mathbf{u}_{t}}+\mathbf{K}_{t}^{T} \mathbf{Q}_{\mathbf{u}_{t}, \mathbf{u}_{t}} \mathbf{k}_{t} \\ &V\left(\mathbf{x}_{t}\right)=\text { const }+\frac{1}{2} \mathbf{x}_{t}^{T} \mathbf{V}_{t} \mathbf{x}_{t}+\mathbf{x}_{t}^{T} \mathbf{v}_{t} \end{aligned}$

ilqr

backward

$\begin{aligned} &Q_{\mathrm{x}}=\ell_{\mathbf{x}}+\mathbf{f}_{\mathbf{x}}^{\top} V_{\mathbf{x}}^{\prime}\\ &Q_{\mathbf{u}}=\ell_{\mathbf{u}}+\mathbf{f}_{\mathbf{u}}^{\top} V_{\mathbf{x}}^{\prime}\\ &Q_{\mathrm{xx}}=\ell_{\mathbf{x} \mathbf{x}}+\mathbf{f}_{\mathbf{x}}^{\top} V_{\mathbf{x}}^{\prime} \mathbf{f}_{\mathbf{x}}+V_{\mathbf{x}}^{\prime} \cdot \mathbf{f}_{\mathbf{x} \mathbf{x}}\\ &Q_{\mathrm{uu}}=\ell_{\mathbf{u u}}+\mathbf{f}_{\mathbf{u}}^{\top} V_{\mathbf{x x}}^{\prime} \mathbf{f}_{\mathbf{u}}+V_{\mathbf{x}}^{\prime} \cdot \mathbf{f}_{\mathbf{u u}}\\ &Q_{\mathrm{ux}}=\ell_{\mathbf{u x}}+\mathbf{f}_{\mathbf{u}}^{\top} V_{\mathbf{x x}}^{\prime} \mathbf{f}_{\mathbf{x}}+V_{\mathbf{x}}^{\prime} \cdot \mathbf{f}_{ux} \\ \\ \delta u^{*} &=\underset{\delta u}{\arg \min } Q(\delta x, \delta u)=-Q_{u u}^{-1}\left(Q_{u}+Q_{u x} \delta x\right) \\ &=\mathbf{k}+\mathbf{K} \delta x \\ \mathbf{K} &=-Q_{u u}^{-1} Q_{u x} \\ \mathbf{k} &=-Q_{u u}^{-1} Q_{u} \\ \Delta V(i) &=\quad-\frac{1}{2} Q_{\mathbf{u}} Q_{\mathbf{u u}}^{-1} Q_{\mathbf{u}} \\ V_{\mathbf{x}}(i) &=Q_{\mathbf{x}}-Q_{\mathbf{u}} Q_{\mathbf{u u}}^{-1} Q_{\mathbf{u x}} \\ V_{\mathbf{x x}}(i) &=Q_{\mathbf{x x}}-Q_{\mathbf{x u}} Q_{\mathbf{u u}}^{-1} Q_{\mathrm{ux}} \end{aligned}$

因子图

Factor graphs and GTSAM: A hands-on introduction
Factor graphs for robot perception.

dynamics with contact

contact invariant optimization

shooting 和collocation方法能比较方便应用于无碰撞的控制过程。而对于有接触的有碰撞过程则不适用，比如机械臂和人形机器人的交互。碰撞没有梯度。