轨迹优化之

elastic band
chomp
stomp
trajopt
itomp

轨迹优化的层次：安全，轨迹平滑，控制可行。运动规划侧重前两个，最优控制侧重后两个。而在轨迹规划既涉及到运动规划，又涉及到最优控制，因此概念上覆盖全部的三个层次。

collision-free：
kinematically feasible
dynamically feasible

优化的方法：区别在与对约束函数或者是目标函数的整理。类似于直接计算并不太好计算，而是进一步整理成另一种更加容易计算或者是更加高效的形式

2021 - Integrating Fast Regional Optimization into Sampling-based Kinodynamic Planning for Multirotor Flight

intro

use kinodynamic rrt* as the heuristic plan, then optimized by a regional trajectory optimizer
this optimizer is a sequence of QP problem
regional trajectory optimizer reference:

related workd

regional optimization: consider the local domain information, such as CHOMP

problem: inefficient for narrow passage situation

methodogy

k-rrt*:

solve BVP by Pontryagin Maximum Principle, obtaining the optimal transition time τ∗ and deriving the unconstrained optimal transition rajectory as a 5th-degree polynomial.
check collision, if the path is violated, then relax τ to get a new polynominal

quadratic objective function:

smoothness cost: squared jerk
resemblance cost: distance to original trajectory
collision cost: distance to some anchor point, which providing dragging force to draw the collided part to nearby collision-free areaas

$\begin{aligned} J_{c} &=\sum_{a p \in A P s} \int_{t_{s, a p}}^{t_{e, a p}}\left[p(t)-p_{a p}(t)\right]^{2} d t \\ &=\sum_{a p \in A P s} \sum_{i \in L}\left(\mathbf{c}_{i}-\mathbf{c}_{i}^{a p}\right)^{\top} \int_{t_{s, i, a p}}^{t_{c, i, a p}} \mathbf{t t}^{\top} d t\left(\mathbf{c}_{i}-\mathbf{c}_{i}^{a p}\right) \\ &=\sum_{a p \in A P s}\left(\mathbf{c}-\mathbf{c}^{a p}\right)^{\top} \mathbf{Q}_{c, a p}\left(\mathbf{c}-\mathbf{c}^{a p}\right) \end{aligned}$

iteractive optimization process

solve the quadratic objective iteractively
it cillides with new obstacles, adding new attracting points to provide accurate dragging force
if the state and control violate saturations, increase time duration
selection of the attracting points: 标记轨迹中碰撞区域（更高维度中很难决定哪些区域是碰撞的）的起点和终点，通过A 快速找到一条无碰撞路径。选取碰撞轨迹区段中点与A路径中点向外延伸作为attracting point.,通过局部选择牵引点的方式避免计算碰撞梯度

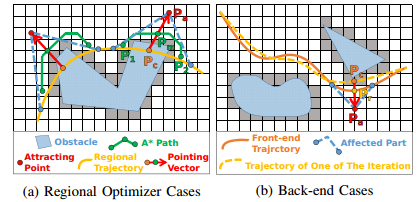
overview

对于障碍物的表达：使用A* 选取牵引点，以与牵引点的距离作为优化梯度避开障碍物

trajectory refinement

trajopt

introduction

use l1 penalties for equality and inequality
computed signed distance using convex-convex collision detection

轨迹优化是最优控制中的一个基本概念。

potential field
CHOMP
STOMP
ITOMP

Sequential Convex Optimization

solves a non-convex optimization problem by repeatedly constructing a convex subproblem—an approximation to the problem around the current iterate x

turning the infeasible constraints into penalty:

$g_i(x) \leq 0 \quad \longrightarrow \quad |g_i(x)|^+ \\ h_i(x) =0 \quad \longrightarrow \quad |h_i(x)| \\ \text{where}\quad |x|^+ = \max(x,0)$

two loops:

outer loop(PenaltyIteration): increase the penalty coefficient µ until all the constraints are satisfied
next loop(ConvexifyIteration): repeatedly construct a convex approximation to the problem

l2 VS l1:

stomp

moveit 三种轨迹优化方法对比

Time-optimal Trajectory Parameterization
Iterative Spline Parameterization
Iterative Parabolic Time Parameterization

time optimal path

2014-TOPP

A General, Fast, and Robust Implementation of the Time-Optimal Path Parameterization Algorithm

introduction

three families of methods：

dynamic programming: divide the$(s, \dot{s})$ plane into a grid and find the optimal trajectory in the $(s,\dot{s})$ plane
convex optimization: discretize the s-axis into N segments and subsequently convert into a convex optimization problem
numerical integration: Pontryagin Maximum Principle(庞特里雅金极大原理 ), the optimal trajectory in the $(s, \dot{s})$ plane is known to be “bang-bang” and can thus be found by integrating successively the maximum and minimum accelerations $\ddot{s}$. But the programming is difficult with the so-called dynamic singularities

This paper develops a numerical integration method considering the dynamic singularities.

bang-bang control: 起停式控制，有迟滞区间。在最优控制中，若最优控制信号为其上限或下限，则该最优控制问题可以以起停式控制为最优解。起停式控制常出现在最短时间的最佳控制问题中[2]。例如要车辆行驶一定距离，且从出发到最后停止的时间要最短，其解法是在经过某一“切换点”前用最大油门加速，过切换点后以最大刹车方式刹车，让车停在想要的位置。---- wiki

improve the robustness of the numerical integration approach

General formulation of the TOPP problem: