optimization
矩阵理论
YeeKal
•
•
"#optimization"
矩阵空间
- $C(A)$: 列空间
- $C(A^T)$: 行空间
- NULL(A): 零空间
- NULL(A^T): 左零空间
- 行空间和零空间的维度只和为n
- 列空间和左零空间的维度只和为m
- 行空间和零空间正交(Orthogonality)
把矩阵写成行空间的向量组合, 则由零空间可推出行空间和零空间正交:
线性空间投影: $Ax = b$
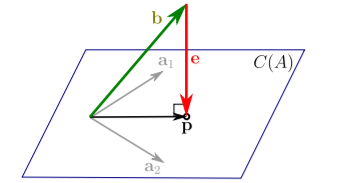
b是A的列空间的线性组合, 若b中包含了左零空间中的维度($b= p+ e$),则方程无解。但可以通过投影找到最近的解,即方程退化为$Ax = p$
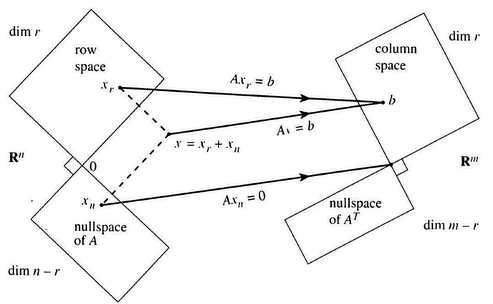
x的基础解系是A的行空间的线性组合, 而x可以由零空间拓展成无数个解。
最小二乘法(Least Squares, LS)
$Ax = b$, 若无解, 则找到b在列空间的投影p。 使得Ax = p, 则p是距离b最近的解。
- br: 列空间
- bn: 左零空间
- 垂直
- 水平
- 广义最小二乘: Generalized Least Squares, GLS
- 非线性扩展
投影矩阵
其中$a^Ta$为标量,为了归一化