02-classification

Classification problem. For now, we will focus on the binary classification problem in which $y$ can only takes two values, 0 and 1.

logistic regression

Change the form for our hypotheses $h_\theta(x)$:

$$h_\theta(x)=g(\theta^T x)=\frac{1}{1+e^{-\theta^Tx}} \\$$

where

$$g(z)=\frac{1}{1+e^{-z}}=\frac{e^z}{1+e^z} \\$$

is called the sigmoid function or logistic function. Here is a plot showing $g(z)$:

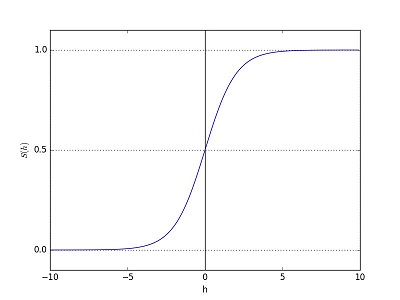
We suppose y=1 when $h_\theta \ge 0.5$, which means $\theta^Tx \ge 0$. Consider logistic regression has two features $x_1$ and $x_2$, when $\theta^Tx = 0$, $\theta_0+\theta_1 x_1+\theta_2x_2=0$. So in the $x_1-x_2$ plane, the seperation is a line, which is called decision boundary. However, if two features with quadratic polynomial, the boundary is non-linear and may be a circle. In higher order polynomial, the shape is more complex.

The choice of the logistic function is a fairly natural one(why?). One useful property of the derivative of the sigmoid function:

$$g'(z)=g(z)(1-g(z)) \\$$

Let us assume that:

$$P(y=1|x;\theta)=h_\theta(x)\\P(y=0|x;\theta)=1-h_\theta(x) \\$$

or:

$$p(y=1|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y} \\$$

the maximum likelihood estimation:

$$\begin{align}L(\theta)&=\prod_{i=1}^mp(y^{(i)}|x{(i)};\theta)\\&=\prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}\end{align} \\$$

$$l(\theta)=-logL(\theta)=-\sum_{i=1}^my^{(i)}logh(x^{(i)})+(1-y^{(i)})log(1-h(x^{(i)})) \\$$

$$\begin{align}\frac{\partial}{\partial\theta_j}l(\theta) &=\frac{\partial l}{\partial h_{\theta}(x)} \frac{\partial h_{\theta}(x)}{\partial z} \frac{\partial z}{\partial \theta_j} \\ &=\sum_{i=1}^m (-\frac{y^i}{h_\theta(x)}-+\frac{1-y^i}{1-h_\theta(x)})\cdot h_\theta(x)(1-h_\theta(x))\cdot x_j \\ &=\sum_{i=1}^m(-y^i(1-h_\theta(x))+(1-y^i)h_\theta(x))\cdot x_j \\ &=-\sum_{i=1}^m (y^i-h_\theta(x^i))x^i_j \end{align}$$

This therefor gives us the stochastic ([sto'kæstɪk]随机的) gradient ascent rule:

$$\theta_j:=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)} \\$$

It has identical expression compred with LMS.

In fact, they are all aimed to get the maximum likelihood. To get the maximum number, we are supposed to find the solution of the first-order derivative. So the problem is thansfered to finding the solution of $f(x)=0$. think about your Numerical Analysis(数值分析)

Considerating Newton's method:

$$\theta:=\theta-\frac{f(\theta)}{f'(\theta)}\quad\to\quad \theta:=\theta-\frac{l'(\theta)}{l''(\theta)} \\$$

a more general form (also called the Newton-Raphson method):

$$\theta:=\theta-H^{-1}\bigtriangledown_\theta l(\theta) \\$$

where $H$ is the Hessian matrix, whise entries are given by:

$$H_{ij}=\frac{\partial^2l(\theta)}{\partial \theta_i\partial \theta_j} \\$$

Newton's method typically enjorys faster convergence.

Fisher's LDA

linear discriminant analysis(线性判别分析)

ref

• 由Logistic Regression 所联想到的