Optimization based path planning for car parking in narrow environments

Abstract

a static optimization problem is formulated
a tree-based guidance for the local planner

本文把泊车的运动规划问题看成一个静态的优化问题(a static optimization problem)来处理，同时考虑了在无碰撞的情况下尽可能得提高可行使长度。对于狭窄场景，提出了基于树采样进行引导(a tree-based guidance)规划的方法。

所谓a static optimization problem, 笔者理解为不考虑速度，只考虑路径；障碍物都当作静态障碍物的场景。

Introduction

build roadmap
rrt with kinematic constraints, Integrating the differential equations of the robot for a specified distance
1. randomised inputs¹
2. inputs based on the analytic solution²
geometry
- Dubins
- Reeds and Shepp
- β-spline, Bezier or polynomial [17] curves
hybrid a-star
non-holonomic characteristics
- small-time-controllable
- chained-form systemand sinusoidal inputs
- Dubins curves
- clothoid curves
optimal control problem

文中先是列举了常用的规划方法，并提出以上方法可能对某些场景或者单一泊车场景有效果，但是对于更加泛化和多元化的，以及狭窄空间下的停车场景也许无法计算出有效轨迹。因此本文提出了一种基于优化方法的泊车规划器，能够以较低的计算代价实现狭窄场景下的实时规划。

Problem statement

本文首先讨论了普通场景下的三种车位的规划方法，即

parallel slot: 水平车位，侧方位停车
garage slot：垂直车位，倒车入库
angle slot：斜列车位

后面又更深入扩展了规划器再狭窄场景下和比较杂乱的停车场(parking deck)下的规划方法

图片引用自原论文

根据自行车模型，把状态量对时间求导，可列出小车的动力学方程：

$\left\{\begin{align} \dot{x} &=v\cdot cos(\theta) \\ \dot{y} &=v\cdot sin(\theta) \\ \dot{\theta} &=\frac{v \cdot tan(\phi)}{L} \\ \dot{v} &= a \\ \dot{\phi} &= \zeta\ \end{align}\right.$

而在本文中，只考虑轨迹，不考虑时间上的速度和加速度。把状态量对时间求导改为对轨迹长度求导。

对于任一变量 a: $\frac{da}{ds} = \frac{da}{dt} \frac{dt}{ds} = \frac{1}{v}\frac{da}{dt}$

则状态方程转化为：

$\left\{ \begin{align} \dot{x} &= cos(\theta) \\ \dot{y} &=sin(\theta) \\ \dot{\theta} &=\frac{tan(\phi)}{L} \end{align} \right.$

其中注意到$\frac{tan(\phi)}{L}$实际就是由于方向盘转弯而导致的曲率,对于自行车模型.曲率和方向盘转角是一一对应的,因此运动学模型也可以写为:

$\left\{\begin{align} \dot{x} &= cos(\theta) \\ \dot{y} &=sin(\theta) \\ \dot{\theta} &=u_l \end{align}\right.$

这样就得到文中的方程式：

$\mathbf{q}^{\prime}=\left(\begin{array}{c} x^{\prime} \\ y^{\prime} \\ \theta^{\prime} \end{array}\right)=\left(\begin{array}{c} D \cos (\theta) \\ D \sin (\theta) \\ D u_l \end{array}\right)=\mathbf{f}_s\left(\mathbf{q}, u_l, D\right)$

其中$D\in{-1, 1}$指示车行驶的方向，1代表向前，-1代表向后。

Path Planning for Car Parking

对于上述非线性方程，根据路径s进行二阶离散。注意这里步长$\eta_i\in[\eta_{min}, \eta_{max}]$也是一个变量。得到如下表达式：

$\begin{aligned} \mathbf{q}_{i+1} & =\left(\begin{array}{l} x_{i+1} \\ y_{i+1} \\ \theta_{i+1} \end{array}\right)=\left(\begin{array}{c} x_i+D \eta_i \cos \left(\theta_i+D \frac{\eta_i u_{l_i}}{2}\right) \\ y_i+D \eta_i \sin \left(\theta_i+D \frac{\eta_i u_{l_i}}{2}\right) \\ \theta_i+D \eta_i u_{l_i} \end{array}\right) \\ & =\mathbf{f}\left(\mathbf{q}_i, \mathbf{u}_i, D\right) . \end{aligned}$

上式中，$D$作为指示方向的变量可以忽略。除去状态变量$[x, y, \theta]$之外，还有两个变量，即$u=[u_l, \eta]$, 表示方向盘转角(实际为曲率)和步长，作为优化变量。

文中的优化问题并不是一次优化完整条轨迹，而是每次走一步，循环迭代直到判断需要换挡的位置。该优化问题定义为：

$\begin{array}{ll} \min _{\mathbf{u}_i} & l_{O_i}\left(\mathbf{q}_{i+1}\right) \\ \text { s.t. } & \mathbf{q}_{i+1}=\mathbf{f}\left(\mathbf{q}_i, \mathbf{u}_i, D\right) \\ & \mathbf{h}_P\left(\mathbf{q}_{i+1}\right) \leq \mathbf{0} \\ & \mathbf{u}_{\min } \leq \mathbf{u}_i \leq \mathbf{u}_{\max }, \end{array}$

其中损失函数： $\begin{aligned} l_{O_i}\left(\mathbf{q}_{i+1}\right)&=r_\theta e_{\theta_{i+1}}^2+\mathbf{e}_{P_{i+1}}^{\mathrm{T}} \mathbf{R e}_{P_{i+1}}+r_u \Delta u_i^2 \\ e_{p_i}&=[x_i-x_E, y_i-y_E]^T &\text{目标点的位置偏差} \\ e_{\theta_i}&=\theta_i-\theta_O & \text{预定义目标的航向偏差} \\ \Delta u_i &=u_i-u_{i-1} & \text{方向盘转角变化} \\ r_\theta,& R, r_u & 权重系数 \end{aligned}$

约束函数中，第一项为状态方程，第二项为碰撞检测，第三项为控制参数变化范围。

文中没有对碰撞检测做更加详细的说明，只提到使用了Minkowski sum³.

在规划的具体实施上，文中提出了分两步走的策略，其中定义了一个方便脱困的中间转换点(Phase switching point)$q_P$.整个规划是倒着从库内到库外规划，因此两步规划分别为： 1. phase B: $q_E\rightarrow q_P$,从终点到转换点 2. phase A: $q_P\rightarrow q_S$,从转换点到起点

图片引用自原论文

在phase B状态,规划器尽量找到能使自车到达一个方便脱困的位置的轨迹.在垂直和斜列车位,只需要保持航向不变,前进或后退到某个点. 而对于水平车位车需要摆过一定的角度才方便从库位内脱困出来(如下图水平车位的Phase switching point).

图片引用自原论文

因此在phase B的规划阶段,目标航向的变化在垂直和斜列场景设为0,而在水平场景设置为$\frac{\pi}{2}$: $\theta_O = \theta_P + \gamma \\ \gamma= \begin{cases}+ \frac{\pi}{2} & \text { for parallel parking from left }\\ -\frac{\pi}{2} & \text { for parallel parking from right} \\ 0 & \text { else }\end{cases}$

同时在权重系数设置上,对于航向误差设置较大的参数,位置误差设置为0,使得优化器能尽快摆到脱困的航向位姿.(水平的目标航向不设置为$q_P$的航向,猜测$q_P$不是个定点,因此才把目标航向设置的比较大,让优化器尽力朝着脱困的航向优化)

在phase A:$q_P\rightarrow q_S$阶段,起点$q_S$被当作目标点. 坐标系设置为以$q_S$为原点,x为纵向,y为横向.目标点航向为0. 在该阶段, y方向和航向误差的参数设置的比较大,而在行驶方向--即x方向上的参数比较小.

switching point的计算

文中把转换点分为两类,一类是上文提到的phase switching point, 另一类是driving switching point, 是指在同一phase的轨迹规划内的前进和倒退的换档点.

phase switching point的计算: 在垂直和斜列车位场景是让车沿直线开出一定距离,而水平是当左前角点突出一定距离之后认为是可以脱困的点.

图片引用自原论文

driving switching point的计算, rule1:当遇到障碍物没有足够的行驶空间的时候就是换档的时期. 这一条规则在phase B和phase A都适用.在phase B中,主要存在于水平车位场景,即当水平车位较窄时,可能需要在库内多次换档.在这一阶段的优化中,当遇到障碍物没有足够的行驶空间的时候就换档,如此循环直到满足脱困条件.
driving switching point的计算, rule2:当最优解的损失函数开始增大的时候($l^_{O_i}>l^{O$)标志着需要换档了.主要针对phase A场景.文中以下图解释如此操作的原因.下图从$q_P$到switching point的过程中,y方向和航向与目标点的偏差逐渐缩小,因此这两方面的损失也迅速减小.而x方向的误差逐渐增大,损失函数也逐渐增大,总的损失函数趋近减小. 当y方向和航向趋近于0的时候,$q_P$和switching point基本在一条直线上,这也是较好的换档位置.同时由于y方向和航向的权重参数比较大,在这一位置,如果再往前则总的损失函数趋近增大,因此可以通过$l^}_{O_i}>l^{O$来判断是否是比较好的换挡位置.}

图片引用自原论文

到这里,文中已经完整描述了一个完整的针对泊车的基于优化的轨迹规划的方法.优化的方法一般需要比较好的初始值才能很好得收敛到最优解.这种优化方法是一次性优化整条路径.但是本文不使用初始轨迹,而是每次优化只往前迭代一步,通过cost function引导路径走向终点.全局路径的优化方法难以处理换档点,而本文提出的方法可以在迭代过程中根据当前的状态判断是否需要换档.

全局优化
- 优化整条轨迹
- 需要初始值
- 无法处理换档点
本文的分步优化
- 优化当前的一步
- 不需要初始值
- 能处理换档点

但是正因为每次只向前走一步,因此无法把握全局的环境信息,路径不一定最优. 对换档点的判断处理过于简单,会导致非常多的换档点.下图是一个简单场景下求解失败的例子.当从起点走到P点,y和theta误差都在迅速下降,cost减小. 但是y和theta误差可能不是同步到达最小值,因此会由于cost的增加而提前换档,这个时候继续往前会很快又到达换档点,因此会无故增加很多次换档.

正因为如此,文中又提出了在狭窄场景下的引导树构建方法. 本小节中的方法(主要是phase A阶段的规划)会作为通用的局部规划器在下一节描述的方法中用到。

靠近终点时会出现多次无效换档

Path Planning in Narrow Environments

采样关键点的方法一般会用来应对复杂场景中的运动规划，而对于非完整性约束(non-holonomic)的系统，采样法又存在几个难点：1. 无碰撞 2. 微分方程约束的可达性 3. 距离衡量。因此这种方法经常需要大量的采样点以及计算耗时。

根据人类泊车的经验，文中针对泊车场景提出了一种高度定制化的采样方法。对于停车场的道路环境，以及人类开车的习惯，泊车时一般会走直线移动一段距离(parallel displacement)或者打弯走向垂直方向的某个位置(orthogonal displacement)。基于以上先验认知，文中提出了以当前起始点$q_0$沿水平方向的水平采样点$q_{R_P}$,和沿垂直方向的垂直采样点$q_{R_O}$,如下图所示：

图片引用自原论文

$\mathbf{q}_{R_P}=\mathbf{q}_0+\left[\begin{array}{c} \Delta x+\sigma_{x_P} \\ \sigma_{y_P} \\ \sigma_{\theta_P} \end{array}\right], \quad \mathbf{q}_{R_O}=\mathbf{q}_0+\left[\begin{array}{c} \Delta x+\sigma_{x_O} \\ \sigma_{y_O} \\ \pm \frac{\pi}{2}+\sigma_{\theta_O} \end{array}\right]$

其中$\sigma_{\xi_j}, \xi\in {x, y, \theta}, j \in {P, O}$表示采样时加入的均匀分布误差，在不同的方向上有不同的取值。比如$\sigma_{y_O}$一般取值比较大，而$\sigma_\theta$取值比较小。$\Delta x$是一个常量来保证有足够的行使距离。

这些采样点无需保证是无碰撞或者是可达的，它们的作用只是给出一个探索的方向。连接当前点与采样点的轨迹依靠上述提到的优化方法来进行，秉持“走一步算一步”的策略保证轨迹的无碰撞和可达性。

在采样之后，以采样点为导向，由$q_0$计算出对应的采样轨迹以及真实可达的实际采样点(又可以称为关键点，注意这里的点也包括局部规划路径上的中间换挡点)$q_L$, 同时对实际采样点进行代价计算. 对于任意一个关键点$q_L$, 代价函数为:

$\begin{aligned} l_L &=\mathbf{e}_{\mathbf{q}_L}^{\mathrm{T}} \mathbf{R}_L \mathbf{e}_{\mathbf{q}_L}+r_l P_l+r_{S P} N_{S P} \\ e_{q_l}&:\quad \text{与终点的位姿偏差} \\ P_{l}&:\quad \text{当前为止的路径长度} \\ N_{sp}&:\quad \text{当前为止的换挡次数} \end{aligned}$

若实际采样点能连接到最后的终点，则规划成功，否则把这些点加入到候选集中，根据代价函数循环进行下一次采样。整体规划思路如下：

图片引用自原论文

下图展示了一次采样的例子。其中$q_{L_1}$是以水平采样点$q_{R_P}$为导向由局部规划器生成的对应于水平方向上的实际采样点。$q_{L_2}, q_{L_3}, q_{L_4}$是以垂直采样点$q_{R_O}$为导向由局部规划器生成的对应于垂直方向上的实际采样点，而$q_{L_2}, q_{L_3}$又是局部轨迹上的换挡点。

仿真结果

水平+垂直+斜列的普通泊车场景：图片引用自原论文

垂直车位的杂乱场景（虚线为Hybrid A*的结果）：图片引用自原论文

垂直车位的狭窄场景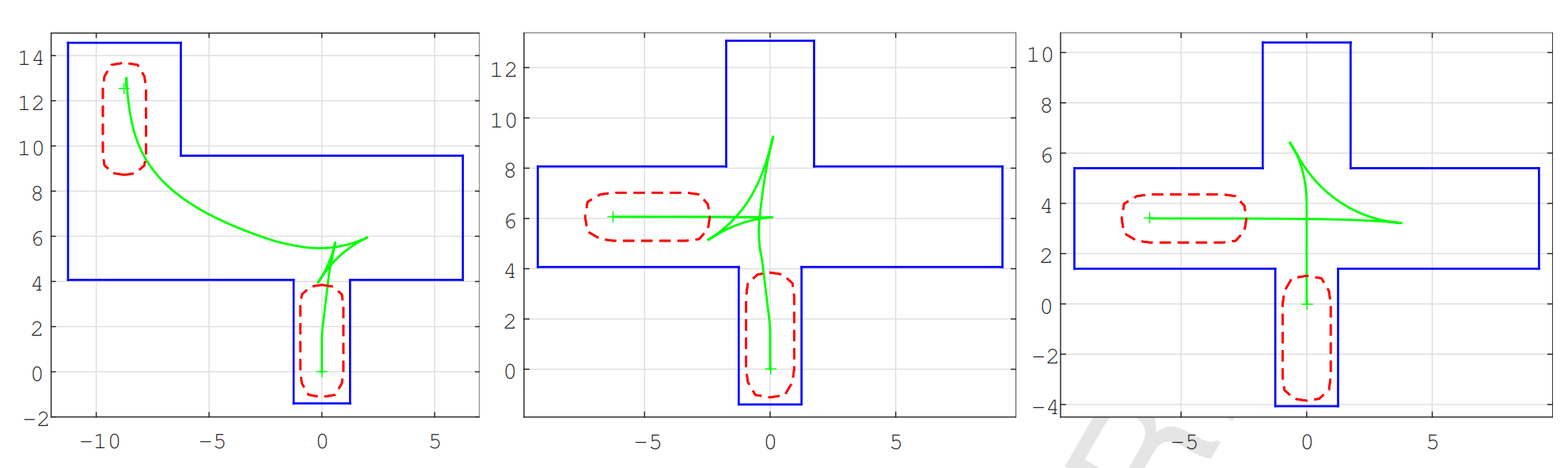：图片引用自原论文

总结

本文提出了一种操作性强，极具定制化的基于优化的泊车运动规划算法。由于优化过程是单步优化，因此求解速度比较快，同时方便判断换挡时机。但也因为缺少全局优化项，难以求得最优路径，这在文中的实验中也体现了出来，即相比于Hybrid A*有更长的路径和更多的换挡次数。在另一篇实践作业中也描述了换挡次数非常多的不合理结果⁴。文中的实验在成功率上相比Hybrid A*有些许提高，但对比不是特别明显。文中提到平均求解时间在20ms左右，并且比较稳定，但是没有给出详细的对比数据。文中基于先验知识提出的采样方法极具借鉴意义。

代码实现

[待填坑]

Ref

2000-Randomized kinodynamic motion planning with moving obstacles ↩
1991-A fast path planner for a car-like indoor mobile robot ↩
Spatial planning: A configuration space approach,” IEEE Trans. Comput., vol. C-32, no. 2, pp. 108–120, 1983. ↩
算法的实践报告 ↩
Optimisation based path planning for car parking in narrow environments ↩