planning
回旋螺线
YeeKal
•
•
"#planning"
螺旋线有很多种,这里讨论的是“曲率随长度线性变化的螺旋线”, 即回旋螺线,又被称为欧拉螺线(Euler Spiral),或者羊角螺线(clothoid)。在现实环境中经常需要曲线的曲率是连续变化的,因此欧拉螺线被广泛用于曲线拟合以及路径规划中。
回旋螺线的参数方程可以写为:
为了计算方便,一般把$\kappa_0$ 设为0,则本文主要讨论的曲线参数方程为:
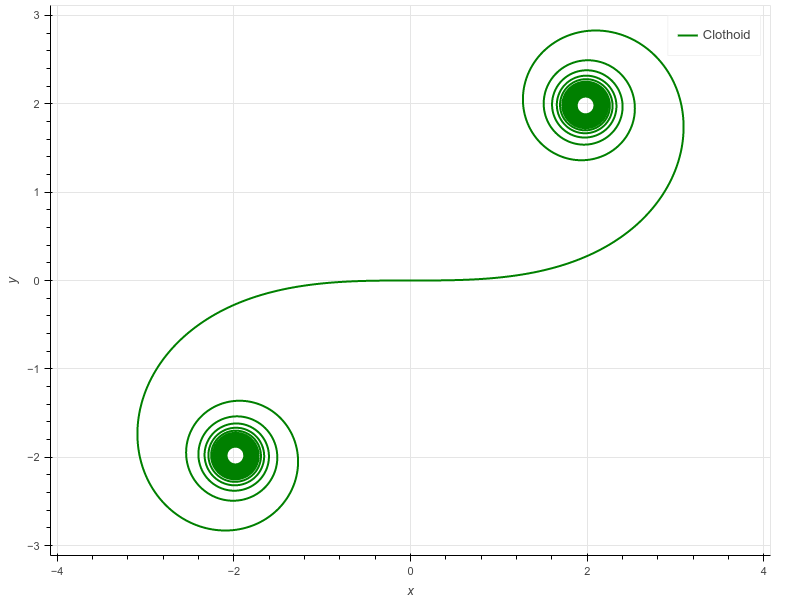
parametrical clothoid(参数螺旋线)
- $\alpha$: sharpness, rate of curvature
- curvature
- deflection
- length
if $\kappa_0 = 0$, then at end:
at middle:
Fresnel integrals:
螺旋线与圆相切

螺旋线与圆相切实际上就是直线过渡到圆的螺旋线路径。
在表达式中$\kappa(s)=\alpha s$,曲率变化率$\alpha$确定之后,则可以通过转弯半径$R$计算出一段从直线过度到圆的螺旋线$C_{OP}$.圆心$c$通过端点$P$的位置以及$\theta$确定。
连接圆心$c$和起点$O$可以得到一个更大的半径$R_l$,螺旋线$C_{OP}$就在这个更大的圆内,并且起点$O$与大圆在$O$点的切线夹角记为$\mu$. 可以看出螺旋线$\vec{OP}$的终点斜率和大圆在X轴处的斜率保持一致。
两圆相切的过渡曲线 CPSPC
由上一节可知螺旋线的出圈点在大圆的弦上,弦和切线的夹角为$\mu$。
